题目内容
函数
的最小正周期为 ，此函数的值域为 。
的最小正周期为 ，此函数的值域为 。
利用二倍角的余弦公式化简函数y=cos2x-sin2x+2sinx?cosx，再化为一个角个一个三角函数的形式，求出函数的最小正周期，和值域．
解：函数y=cos2x-sin2x+2sinx?cosx=cos2x+sin2x=
sin（2x+
）
所以函数函数y=cos2x-sin2x+2sinx?cosx的最小正周期为：
=π
函数的值域为：[
，]
故答案为：π；[，]
解：函数y=cos2x-sin2x+2sinx?cosx=cos2x+sin2x=
sin（2x+）所以函数函数y=cos2x-sin2x+2sinx?cosx的最小正周期为：
=π函数的值域为：[
，]故答案为：π；[
，]
练习册系列答案
阅读快车系列答案
相关题目
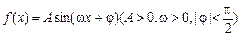的图象在y轴上的截距为1，它在y轴右侧的第一个最大值点和最小值点分别为（
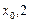）和（
）.
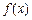的解析式；
,
图象向左平移
个单位长度后，所得曲线的一部分，如图所示，则
为（ ）
,
,且
．
且
，求
的值；
＝
，求
的最小正周期及单调增区间；
的图象按向量
平移后得到函数
的图象，求
的图象如图所示，则
的表达式是
.
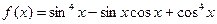，则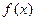
的值域是 。
．
的最小正周期；
时，求函数
相应的取值．