题目内容
已知椭圆与双曲线x2-
=1有公共的焦点,且椭圆过点P(0,2).
(1)求椭圆方程的标准方程;
(2)若直线l与双曲线的渐近线平行,且与椭圆相切,求直线l的方程.
| y2 | 3 |
(1)求椭圆方程的标准方程;
(2)若直线l与双曲线的渐近线平行,且与椭圆相切,求直线l的方程.
分析:(1)求出双曲线x2-
=1 的焦点坐标分别为(-2,0)(2,0),即c=2;设出椭圆的标准方程,利用椭圆过点P(0,2),求出a2,b2;
(2)双曲线渐近线方程是y=±
x,设直线l:y=±
x+m,根据直线与椭圆相切解出m的值.
| y2 |
| 3 |
(2)双曲线渐近线方程是y=±
| 3 |
| 3 |
解答:解:(1)设椭圆方程为
+
=1 (a>b>0).
双曲线x2-
=1 的焦点坐标分别为(-2,0)(2,0),
∴椭圆焦点坐标分别为(-2,0)(2,0),∴c=2,即a2=b2+4,
又椭圆过点P(0,2),则0+
=1,
∴b2=4,得a2=8,
∴所求椭圆方程的标准方程为
+
=1;
(2)双曲线渐近线方程:y=±
x,
设直线l:y=±
x+m,
代入椭圆方程得:7x2±4
mx+2m2-8=0,
由相切得:△=48m2-28(2m2-8 )=0,解得m=±2
∴直线l的方程是:y=±
x±2
.
| x2 |
| a2 |
| y2 |
| b2 |
双曲线x2-
| y2 |
| 3 |
∴椭圆焦点坐标分别为(-2,0)(2,0),∴c=2,即a2=b2+4,
又椭圆过点P(0,2),则0+
| 4 |
| b2 |
∴b2=4,得a2=8,
∴所求椭圆方程的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)双曲线渐近线方程:y=±
| 3 |
设直线l:y=±
| 3 |
代入椭圆方程得:7x2±4
| 3 |
由相切得:△=48m2-28(2m2-8 )=0,解得m=±2
| 7 |
∴直线l的方程是:y=±
| 3 |
| 7 |
点评:本题考查了双曲线的简单性质与椭圆的标准方程,考查了直线与椭圆的位置关系,解答的关键是利用直线与椭圆相切的条件△=0求出待定系数.

练习册系列答案
相关题目
 .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积. 与双曲线
与双曲线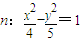 有两个公共点,且椭圆m与双曲线n的离心率之和为2.
有两个公共点,且椭圆m与双曲线n的离心率之和为2.