题目内容
在下列约束条件下: 求目标函数f=4x-y的最大值和最小值.
求目标函数f=4x-y的最大值和最小值.
解:不等式组在平面上表示的区域B如下图阴影部分所示.
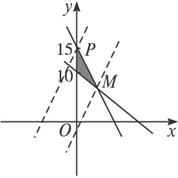
将目标函数f=4x-y改写成y=4x-f.
原命题![]() 在区域B里寻找一点(x,y),使得该点的斜率为4的直线纵截距(-f)最大或最小,
在区域B里寻找一点(x,y),使得该点的斜率为4的直线纵截距(-f)最大或最小,
从而使目标函数f在点(x,y)处取得最小或最大值.
显然过P点的斜率为4的直线有最大纵截距-f=15,
所以目标函数在点(0,15)取得最小值f=-15.
过M点的斜率为4的直线纵截距(-f)取得最小值,从而目标函数f取得最大值.
由![]()
![]() 交点M(4,5),
交点M(4,5),
所以目标函数f的最大值f=16-5=11.

练习册系列答案
相关题目
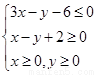 下
,目标函数
下
,目标函数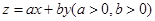 的最大值为12.给出下列四个判断:
的最大值为12.给出下列四个判断: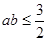 ; ②
; ②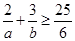 ; ③
; ③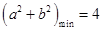 ; ④
; ④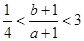 .
.