��Ŀ����
��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��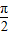 ����ͼ���y�ύ�ڣ�0��1����y���Ҳ�ĵ�һ�����ֵ����Сֵ��ֱ�ΪP��x��2����Q��x+3�У�-2����
����ͼ���y�ύ�ڣ�0��1����y���Ҳ�ĵ�һ�����ֵ����Сֵ��ֱ�ΪP��x��2����Q��x+3�У�-2������1������y=f��x���Ľ���ʽ��x��
��2������y=f��x���ĵ����ݼ����䣻
��3�������y=f��x��ͼ�������е�ĺ��������̵�ԭ����
 �������겻�䣩��Ȼ���ٽ�����ͼ����x�Ḻ����ƽ��
�������겻�䣩��Ȼ���ٽ�����ͼ����x�Ḻ����ƽ��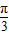 ����λ�����y=f��x��ͼ�������е�����������̵�ԭ����
����λ�����y=f��x��ͼ�������е�����������̵�ԭ���� �������겻�䣩�õ�����y=g��x����ͼ��д������y=g��x���Ľ���ʽ������y=|g��x��|�ĶԳ��᷽�̣�
�������겻�䣩�õ�����y=g��x����ͼ��д������y=g��x���Ľ���ʽ������y=|g��x��|�ĶԳ��᷽�̣�
���𰸡���������1����y���Ҳ�ĵ�һ�����ֵ����Сֵ��ֱ�ΪP��x��2����Q��x+3�У�-2���ɵ������ڣ�����������A=2�� ��������ͼ���y�ύ�ڣ�0��1�����ϕ�Ӷ��͵���������ʽ��
��������ͼ���y�ύ�ڣ�0��1�����ϕ�Ӷ��͵���������ʽ��
��2�������Һ����ĵ������䣬���� ��ã�
��ã�
��3�������⣬��������˼·��y=2sin�� ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒g��x��=sin��x+
��⇒g��x��=sin��x+ ����
����
����⣺��1����y���Ҳ�ĵ�һ�����ֵ����Сֵ��ֱ�ΪP��x��2����Q��x+3�У�-2����
T=6�У�A=2�� ��4�֣�
��4�֣�
��x=0����1=2sinϕ
��|ϕ|��
��ϕ= ��5�֣�
��5�֣�
�ຯ��ʽΪy=2sin�� ����6�֣�
����6�֣�
��2���� ��10�֣�
��10�֣�
��+6k��x��4��+2k��k��Z��
�ຯ��y=f��x���ĵ����ݼ�����Ϊ[��+6k�У�4��+6k��]��k��Z����11�֣�
��3��������ã�y=2sin�� ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒g��x��=sin��x+
��⇒g��x��=sin��x+ ����14�֣�
����14�֣�
y=|g��x��|�ĶԳ��᷽��Ϊx=k�У�k��Z����16�֣�
������������Ҫ�������磺f��x��=Asin����x+�գ��и����������弰�䵥���������ͼ��ı任��
 ��������ͼ���y�ύ�ڣ�0��1�����ϕ�Ӷ��͵���������ʽ��
��������ͼ���y�ύ�ڣ�0��1�����ϕ�Ӷ��͵���������ʽ����2�������Һ����ĵ������䣬����
 ��ã�
��ã���3�������⣬��������˼·��y=2sin��
 ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒g��x��=sin��x+
��⇒g��x��=sin��x+ ����
��������⣺��1����y���Ҳ�ĵ�һ�����ֵ����Сֵ��ֱ�ΪP��x��2����Q��x+3�У�-2����
T=6��A=2��
 ��4�֣�
��4�֣���x=0����1=2sinϕ
��|ϕ|��

��ϕ=
 ��5�֣�
��5�֣��ຯ��ʽΪy=2sin��
 ����6�֣�
����6�֣���2����
 ��10�֣�
��10�֣���+6k�С�x��4��+2k�У�k��Z��
�ຯ��y=f��x���ĵ����ݼ�����Ϊ[��+6k�У�4��+6k��]��k��Z����11�֣�
��3��������ã�y=2sin��
 ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒y=2sin��x+
��⇒y=2sin��x+ ��⇒g��x��=sin��x+
��⇒g��x��=sin��x+ ����14�֣�
����14�֣�y=|g��x��|�ĶԳ��᷽��Ϊx=k�У�k��Z����16�֣�
������������Ҫ�������磺f��x��=Asin����x+�գ��и����������弰�䵥���������ͼ��ı任��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ