题目内容
已知p:|1-
|≤2,q:x2-2x+1-m2≤0(m>0),若¬p是¬q的充分而不必要条件,求实数m的取值范围.
| x-1 | 3 |
分析:利用二次不等式与绝对值不等式,分别求解p,q,推出¬p,¬q.利用¬p是¬q的充分而不必要条件,列出关系式,求实数m的取值范围.
解答:解:由x2-2x+1-m2≤0(m>0)得 1-m≤x≤1+m
故¬q:A={x|x<1-m或x>1+m,m>0}
由 |1-
|≤2,得-2≤x≤10
故¬p:B={x|x<-2或x>10}
∵¬p是¬q的充分而不必要条件
∴
解得 0<m≤3
∴实数m的取值范围 0<m≤3
故¬q:A={x|x<1-m或x>1+m,m>0}
由 |1-
| x-1 |
| 3 |
故¬p:B={x|x<-2或x>10}
∵¬p是¬q的充分而不必要条件
∴
|
∴实数m的取值范围 0<m≤3
点评:本题考查绝对值不等式,命题的否定,必要条件、充分条件与充要条件的判断,考查计算能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 ,x∈[
,x∈[ ,4].
,4]. );
); ,
,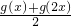 +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围. ,x∈[
,x∈[ ,4].
,4]. );
); ,
, ],则f1(x)=-1,x∈[-
],则f1(x)=-1,x∈[- ,
, ],f2(x)=sinx,x∈[-
],f2(x)=sinx,x∈[- ,
, ],设φ(x)=
],设φ(x)= +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.