题目内容
已知数列{an}为等差数列.(1)若a3=-2,a9=10,则a12=
(2)一般地,若am=s,an=t(m>n),则am+n=
分析:(1)根据第三项和第九项的值得到数列的公差,根据公差和第九项的值得到第十二项的结果.
(2)根据第m项和第n项得到数列的公差,根据第m项和公差得到数列的第m+n项,这是第一问的一般化,见到这样问题解决方法是相同的,等比数列也是这个道理.
(2)根据第m项和第n项得到数列的公差,根据第m项和公差得到数列的第m+n项,这是第一问的一般化,见到这样问题解决方法是相同的,等比数列也是这个道理.
解答:解:(1)设等差数列{an}的公差为d,则a9-a3=6d.
由已知a9-a3=12,
∴d=2
∴a12=a9+3d=16
(2)∵d=
,
则am+n=am+nd
=s+n×
=
.
由已知a9-a3=12,
∴d=2
∴a12=a9+3d=16
(2)∵d=
| s-t |
| m-n |
则am+n=am+nd
=s+n×
| s-t |
| m-n |
=
| ms-nt |
| m-n |
点评:本题主要考查数列的通项,使学生系统掌握解等差数列与等比数列规律,深化数学思想方法在解题实践中的指导作用,灵活地运用数列知识和方法解决数学和实际生活中的有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

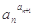 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4