题目内容
是否存在实数a,使函数f(x)=x2-2ax+a的定义域为[-1,1]时,值域为[-2,2]?若存在,求a的值;若不存在,说明理由.
分析:由于函数f(x)=x2-2ax+a的对称轴为 x=a,分a<-1、0>a≥-1、1>a≥0、a≥1 四种情况利用函数的单调性以及定义域、值域求出a的值.
解答:解:由于函数f(x)=x2-2ax+a的对称轴为 x=a,
当a<-1 时,函数f(x)=x2-2ax+a在定义域[-1,1]上是增函数,故有
,
解得 a=-1 (舍去).
当 0>a≥-1 时,函数f(x)=x2-2ax+a在定义域[-1,1]上先减后增,故有
,
解得a=-1.
当 1>a≥0 时,函数f(x)=x2-2ax+a在定义域[-1,1]上先减后增,故有
,
解得a 无解.
当a≥1 时,函数f(x)=x2-2ax+a在定义域[-1,1]上是减函数,
,解得 a 无解.
综上可得,a=-1.
当a<-1 时,函数f(x)=x2-2ax+a在定义域[-1,1]上是增函数,故有
|
解得 a=-1 (舍去).
当 0>a≥-1 时,函数f(x)=x2-2ax+a在定义域[-1,1]上先减后增,故有
|
解得a=-1.
当 1>a≥0 时,函数f(x)=x2-2ax+a在定义域[-1,1]上先减后增,故有
|
解得a 无解.
当a≥1 时,函数f(x)=x2-2ax+a在定义域[-1,1]上是减函数,
|
综上可得,a=-1.
点评:本题考查的知识点是二次函数的性质,函数的最值及其几何意义,其中熟练掌握二次函数的图象和性质,以及二次函数各系数的作用是解答本题的关键,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
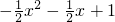 ,f3(x)=2x-1,f4(x)=cosx.;
,f3(x)=2x-1,f4(x)=cosx.;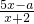 在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.
在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.