题目内容
设F1,F2分别为椭圆 的左、右两个焦点,若椭圆C上的点A(1,
的左、右两个焦点,若椭圆C上的点A(1, )到F1,F2两点的距离之和等于4.
)到F1,F2两点的距离之和等于4.
(1)写出椭圆C的方程和焦点坐标;
(2)过点P(1, )的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
)的直线与椭圆交于两点D、E,若DP=PE,求直线DE的方程;
(3)过点Q(1,0)的直线与椭圆交于两点M、N,若△OMN面积取得最大,求直线MN的方程.
解:(1)椭圆C的焦点在x轴上,
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2,
又点A(1, ) 在椭圆上,因此
) 在椭圆上,因此 ,得b2=1,于是c2=3,
,得b2=1,于是c2=3,
所以椭圆C的方程为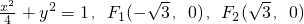 ,…(4分)
,…(4分)
(2)显然直线DE斜率存在,设为k,方程为 ,设D(x1′,y1′),E(x2′,y2′),则
,设D(x1′,y1′),E(x2′,y2′),则
由 ,消去y可得
,消去y可得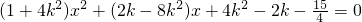
∴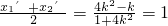 ,∴k=-1
,∴k=-1
∴DE方程为y-1=-1(x- ),即4x+4y=5;…(9分)
),即4x+4y=5;…(9分)
(3)直线MN不与y轴垂直,设MN方程为my=x-1,代入椭圆C的方程得(m2+4)y2+2my-3=0,
设M(x1,y1),N(x2,y2),则y1+y2=-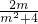 ,y1y2=-
,y1y2=-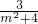 ,且△>0成立.
,且△>0成立.
又S△OMN= |y1-y2|=
|y1-y2|= ×
×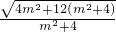 =
=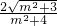 ,
,
设t=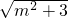 ≥
≥ ,则S△OMN=
,则S△OMN=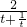 ,
,
(t+ )′=1-t-2>0对t≥
)′=1-t-2>0对t≥ 恒成立,∴t=
恒成立,∴t= 时,t+
时,t+ 取得最小,S△OMN最大,此时m=0,
取得最小,S△OMN最大,此时m=0,
∴MN方程为x=1;…(14分)
分析:(1)把已知点的坐标代入椭圆方程,再由椭圆的定义知2a=4,从而求出椭圆的方程,由椭圆的方程求出焦点坐标.
(2)设出DE方程,代入椭圆方程,利用中点坐标公式,求出斜率,即可求直线DE的方程;
(3)(3)直线MN不与y轴垂直,设MN方程为my=x-1,代入椭圆C的方程,求出△OMN面积,利用导数,确定单调性,可得面积最大值,从而可求直线MN的方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确运用韦达定理是关键.
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2,
又点A(1,
 ) 在椭圆上,因此
) 在椭圆上,因此 ,得b2=1,于是c2=3,
,得b2=1,于是c2=3,所以椭圆C的方程为
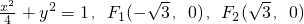 ,…(4分)
,…(4分)(2)显然直线DE斜率存在,设为k,方程为
 ,设D(x1′,y1′),E(x2′,y2′),则
,设D(x1′,y1′),E(x2′,y2′),则由
 ,消去y可得
,消去y可得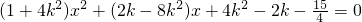
∴
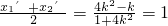 ,∴k=-1
,∴k=-1∴DE方程为y-1=-1(x-
 ),即4x+4y=5;…(9分)
),即4x+4y=5;…(9分)(3)直线MN不与y轴垂直,设MN方程为my=x-1,代入椭圆C的方程得(m2+4)y2+2my-3=0,
设M(x1,y1),N(x2,y2),则y1+y2=-
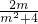 ,y1y2=-
,y1y2=-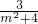 ,且△>0成立.
,且△>0成立.又S△OMN=
 |y1-y2|=
|y1-y2|= ×
×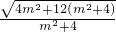 =
=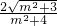 ,
,设t=
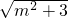 ≥
≥ ,则S△OMN=
,则S△OMN=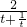 ,
,(t+
 )′=1-t-2>0对t≥
)′=1-t-2>0对t≥ 恒成立,∴t=
恒成立,∴t= 时,t+
时,t+ 取得最小,S△OMN最大,此时m=0,
取得最小,S△OMN最大,此时m=0,∴MN方程为x=1;…(14分)
分析:(1)把已知点的坐标代入椭圆方程,再由椭圆的定义知2a=4,从而求出椭圆的方程,由椭圆的方程求出焦点坐标.
(2)设出DE方程,代入椭圆方程,利用中点坐标公式,求出斜率,即可求直线DE的方程;
(3)(3)直线MN不与y轴垂直,设MN方程为my=x-1,代入椭圆C的方程,求出△OMN面积,利用导数,确定单调性,可得面积最大值,从而可求直线MN的方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确运用韦达定理是关键.

练习册系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点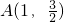 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.