题目内容
已知函数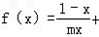 1nx,且m>0.
1nx,且m>0.
(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求m的取值范围;
(Ⅱ)求函数f(x)在[1,e]的最大值和最小值.
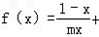 1nx,且m>0.
1nx,且m>0.(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求m的取值范围;
(Ⅱ)求函数f(x)在[1,e]的最大值和最小值.
解:(Ⅰ)求导函数,可得 (m>0).
(m>0).
因为函数f(x)在[1,+∞)上为增函数,
所以f'(x)≥0在[1+∞)上恒成立,
所以mx﹣1≥0在[1,+∞)上恒成立,
所以 上恒成立.
上恒成立.
所以m的取值范围是[1,+∞).
(Ⅱ)令f′(x)=0,∴ (m>0).
(m>0).
①若 <1,即m>1,则x∈[1,e]时,有f'(x)>0,
<1,即m>1,则x∈[1,e]时,有f'(x)>0,
所以f(x)在[1,e]上递增,
所以f(x)的最大值是 的最小值是f(1)=0
的最小值是f(1)=0
②若 <e,即
<e,即 <m≤1,则
<m≤1,则 时,f′(x)<0,
时,f′(x)<0,
所以f(x)在 上递减;
上递减;
 时,f′(x)>0,所以f(x)在
时,f′(x)>0,所以f(x)在 上递增.
上递增.
所以f(x)的最小值是 .
.
又 ,
,
所以当1﹣e+me>0,
即 <m≤1时,有f(e)>f(1),
<m≤1时,有f(e)>f(1),
所以f(x)的最大值是 ;
;
当1﹣e+me≤0,即 时,有f(e)≤f(1),
时,有f(e)≤f(1),
所以f(x)的最大值是f(1)=0.
③若 ,即
,即 ,则x∈[1,e]时,有f'(x)<0,
,则x∈[1,e]时,有f'(x)<0,
所以f(x)在[1,e]上递增,
所以f(x)的最大值是f(1)=0;f(x)的最小值是 .
.
所以f(x)的最大值是 ,
,
f(x)的最小值是
 (m>0).
(m>0).因为函数f(x)在[1,+∞)上为增函数,
所以f'(x)≥0在[1+∞)上恒成立,
所以mx﹣1≥0在[1,+∞)上恒成立,
所以
 上恒成立.
上恒成立.所以m的取值范围是[1,+∞).
(Ⅱ)令f′(x)=0,∴
 (m>0).
(m>0). ①若
 <1,即m>1,则x∈[1,e]时,有f'(x)>0,
<1,即m>1,则x∈[1,e]时,有f'(x)>0,所以f(x)在[1,e]上递增,
所以f(x)的最大值是
 的最小值是f(1)=0
的最小值是f(1)=0②若
 <e,即
<e,即 <m≤1,则
<m≤1,则 时,f′(x)<0,
时,f′(x)<0,所以f(x)在
 上递减;
上递减; 时,f′(x)>0,所以f(x)在
时,f′(x)>0,所以f(x)在 上递增.
上递增.所以f(x)的最小值是
 .
.又
 ,
,所以当1﹣e+me>0,
即
 <m≤1时,有f(e)>f(1),
<m≤1时,有f(e)>f(1),所以f(x)的最大值是
 ;
;当1﹣e+me≤0,即
 时,有f(e)≤f(1),
时,有f(e)≤f(1),所以f(x)的最大值是f(1)=0.
③若
 ,即
,即 ,则x∈[1,e]时,有f'(x)<0,
,则x∈[1,e]时,有f'(x)<0,所以f(x)在[1,e]上递增,
所以f(x)的最大值是f(1)=0;f(x)的最小值是
 .
.所以f(x)的最大值是
 ,
,f(x)的最小值是


练习册系列答案
相关题目
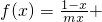 1nx,且m>0.
1nx,且m>0.