题目内容
 设偶函数f(x)的定义域为[-5,5].当x∈[0,5]时,f(x)的图象如图,则不等式f(x)>0的解集为
设偶函数f(x)的定义域为[-5,5].当x∈[0,5]时,f(x)的图象如图,则不等式f(x)>0的解集为分析:先求得不等式f(x)>0在[0,5]上的解集,再根据它的图象关于y轴对称,可得可得不等式f(x)>0在[-5,0]上的解集,综合可得结论.
解答:解:结合函数f(x)在[0,5]上的图象,可得不等式f(x)>0在[0,5]上的解集为(0,2).
再根据f(x)为偶函数,它的图象关于y轴对称,可得可得不等式f(x)>0在[-5,0]上的解集为(-2,0).
综上可得,不等式f(x)>0的解集为 (-2,0)∪(0,2),
故答案为 (-2,0)∪(0,2).
再根据f(x)为偶函数,它的图象关于y轴对称,可得可得不等式f(x)>0在[-5,0]上的解集为(-2,0).
综上可得,不等式f(x)>0的解集为 (-2,0)∪(0,2),
故答案为 (-2,0)∪(0,2).
点评:本题主要考查函数的奇偶性的应用,解不等式,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
设
f(x)是连续函数,且为偶函数,在对称区间[-a,a]上的积分 ,由定积分的几何意义和性质得
,由定积分的几何意义和性质得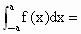
[
]|
A .0 |
B . |
|
C . |
D . |