Question

    在平面直角坐标系xOy中，点_P到定点F（-1，0）的距离的两倍和它到定直线x= -4的距离相等．

    （Ⅰ）求点P的轨迹C的方程，并说明轨迹C是什么图形；

    （Ⅱ）已知点Q（l，1），直线l：y=x+m（m∈R）和轨迹C相交于  A、B两点，是否存在实数m，使△ABQ的面积S最大？若存在，求出m的值；若不存在，说明理由．

Answer 1

解：（Ⅰ）设是点P到定直线的距离，，根据题意，

所求轨迹就是集合.

由此，得.  ………………………………………（3分）

平方化简得，即.         

所以，点P的轨迹是长轴、短轴长分别为，，焦点在x轴上的椭圆.……（6分）

（Ⅱ）设直线和轨迹C相交于、两点.

联立方程得：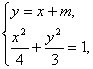

消去，得.

上式有两个不同的实数根，.

且，.       ……………………………………（9分）

于是，.

点Q到的距离为.

所以，的面积

.

当且仅当，即时，，取得最大值，最大值为.