题目内容
在△ABC中,a,b,c分别是角A、B、C的对边 ,且
,且 .
.
(1)求角B的大小;
(2)设函数 ,求函数f(x)的最小正周期,最大值及当f(x)取得最大值时x的值.
,求函数f(x)的最小正周期,最大值及当f(x)取得最大值时x的值.
解:(1)∵ ,且
,且 .
.
∴(2a+c)cosB+bcosC=0
∴2acosB+ccosB+bcosC=0
由正弦定理得2sinAcosB+sinCcosB+cosCsinB=0(2分)
即2sinAcosB+sin(C+B)=0,
∴sinA(2cosB+1)=0,(4分)
在△ABC中,sinA≠0,∴2cosB+1=0,
∵B∈(0,π),∴ (6分)
(6分)
(2)∵ ,∴
,∴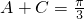
∴ (8分)
(8分)
所以f(x)的最小正周期为π(10分)
令 ,得
,得
即当 ,时f(x)取最大值1 (12分)
,时f(x)取最大值1 (12分)
分析:(1)利用向量的数量积及正弦定理,即可求得角B的大小;
(2)利用辅助角公式化简函数,再利用正弦函数的性质求函数f(x)的最小正周期,最大值及当f(x)取得最大值时x的值.
点评:本题考查解三角形与三角函数的综合,考查向量知识与正弦定理的运用,考查三角函数的性质,属于中档题.
 ,且
,且 .
.∴(2a+c)cosB+bcosC=0
∴2acosB+ccosB+bcosC=0
由正弦定理得2sinAcosB+sinCcosB+cosCsinB=0(2分)
即2sinAcosB+sin(C+B)=0,
∴sinA(2cosB+1)=0,(4分)
在△ABC中,sinA≠0,∴2cosB+1=0,
∵B∈(0,π),∴
 (6分)
(6分)(2)∵
 ,∴
,∴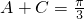
∴
 (8分)
(8分)所以f(x)的最小正周期为π(10分)
令
 ,得
,得
即当
 ,时f(x)取最大值1 (12分)
,时f(x)取最大值1 (12分)分析:(1)利用向量的数量积及正弦定理,即可求得角B的大小;
(2)利用辅助角公式化简函数,再利用正弦函数的性质求函数f(x)的最小正周期,最大值及当f(x)取得最大值时x的值.
点评:本题考查解三角形与三角函数的综合,考查向量知识与正弦定理的运用,考查三角函数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|