题目内容
18.已知点A(1,0),B(0,2),C(3,4).(1)求△ABC面积;
(2)求过此三点圆的方程.
分析 (1)过点C作CD垂直于x轴,交x轴于点D,三角形ABC面积=梯形CDOB面积-三角形AOB面积-三角形ACD面积,求出即可;
(2)分别求出线段AB与线段AC垂直平分线方程,联立求出圆心坐标,再利用两点间的距离公式求出圆的半径,即可确定出所求圆方程.
解答 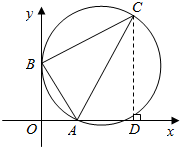 解:(1)过C作CD⊥x轴,交x轴于点D,如图所示,
解:(1)过C作CD⊥x轴,交x轴于点D,如图所示,
根据题意得:S△ABC=S梯形BODC-S△AOB-S△ADC=$\frac{1}{2}$×(2+4)×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×4=9-1-4=4;
(2)∵A(1,0),B(0,2),C(3,4),
∴线段AB的垂直平分线为y-1=$\frac{1}{2}$(x-$\frac{1}{2}$),即2x-4y+3=0,线段AC的垂直平分线为y-2=-$\frac{1}{2}$(x-2),即x+2y-6=0,
联立得:$\left\{\begin{array}{l}{2x-4y=-3}\\{x+2y=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{9}{4}}\\{y=\frac{15}{8}}\end{array}\right.$,即圆心坐标为($\frac{9}{4}$,$\frac{15}{8}$),
∴圆的半径r=$\sqrt{(\frac{9}{4}-1)^{2}+(\frac{15}{8}-0)^{2}}$=$\frac{5\sqrt{13}}{8}$,
则所求圆方程为(x-$\frac{9}{4}$)2+(y-$\frac{15}{8}$)2=$\frac{325}{64}$.
点评 此题考查了圆的标准方程,坐标与图形性质,线段垂直平分线方程,求出圆心坐标与半径是解本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 11000 | B. | 22000 | C. | 33000 | D. | 40000 |
| A. | -4 | B. | -2 | C. | -8 | D. | -6 |

 如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.
如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.