题目内容
已知函数f(x)=sinx+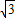 cosx,x∈[0,π].
cosx,x∈[0,π].(1)求f(x)的最大值,并指出取得该最大值时x的值;
(2)求f(x)的单调减区间.
【答案】分析:(1)函数解析式提取2变形后,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域确定出最大值,以及x的值即可;
(2)根据正弦函数的减区间列出关于x的不等式,求出不等式的解集即可确定出f(x)的单调减区间.
解答:解:(1)f(x)=sinx+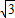 cosx=2sin(x+
cosx=2sin(x+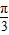 ),
),
∵x∈(0,π),∴x+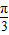 ∈[
∈[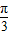 ,
,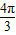 ],
],
则f(x)的最大值为2,
由x+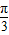 =
=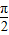 ,解得x=
,解得x=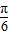 ,
,
则取最大值时的x=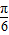 ;
;
(2)由2kπ+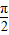 ≤x+
≤x+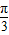 ≤2kπ+
≤2kπ+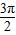 ,k∈Z,
,k∈Z,
解得:2kπ+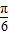 ≤x≤2kπ+
≤x≤2kπ+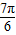 ,k∈Z,
,k∈Z,
又x∈[0,π],
∴f(x)的单调减区间为[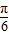 ,π].
,π].
点评:此题考查了两角和与差的正弦函数公式,正弦函数的定义域与值域,以及正弦函数的单调性,熟练掌握公式是解本题的关键.
(2)根据正弦函数的减区间列出关于x的不等式,求出不等式的解集即可确定出f(x)的单调减区间.
解答:解:(1)f(x)=sinx+
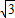 cosx=2sin(x+
cosx=2sin(x+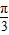 ),
),∵x∈(0,π),∴x+
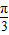 ∈[
∈[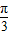 ,
,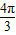 ],
],则f(x)的最大值为2,
由x+
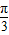 =
=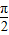 ,解得x=
,解得x=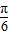 ,
,则取最大值时的x=
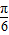 ;
;(2)由2kπ+
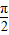 ≤x+
≤x+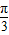 ≤2kπ+
≤2kπ+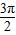 ,k∈Z,
,k∈Z,解得:2kπ+
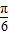 ≤x≤2kπ+
≤x≤2kπ+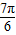 ,k∈Z,
,k∈Z,又x∈[0,π],
∴f(x)的单调减区间为[
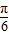 ,π].
,π].点评:此题考查了两角和与差的正弦函数公式,正弦函数的定义域与值域,以及正弦函数的单调性,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
