题目内容
高三(1)班10名学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如下对应数据:x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
如果y与x之间具有线性相关关系,求回归直线方程.
分析:本题数据表中,自变量x的取值没有按从小到大排列,这更接近实际,对结论没有任何影响.从表中看出:同样是每周用16 h学数学,一位同学成绩是64分,另一位却是68分,这反映了y与x只有相关关系,没有函数关系.
解:列出下表,并用科学计算器进行有关计算.
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
xi | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
yi | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
xiyi | 2 208 | 1 185 | 2 231 | 1 691 | 1 024 | 517 | 1 660 | 1 088 | 1 207 | 767 |
| ||||||||||
设回归直线方程为![]() =bx+a,
=bx+a,
则b=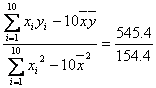 ≈3.53,a=
≈3.53,a=![]() =74.9-3.53×17.4≈13.5,
=74.9-3.53×17.4≈13.5,
因此所求的回归直线方程是=3.53x+13.5.
绿色通道
最小二乘估计是求回归直线方程的常用方法,可以通过本题的解答体会最小二乘估计的优越性.为了计算方便,通常将有关数据列成表格,然后借助于计算器算出各个量,为求回归直线方程扫清障碍.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
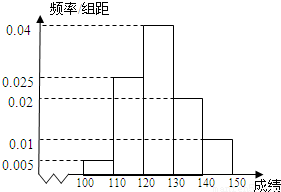
 长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图. 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计得到如下频率分布表:
个组统计得到如下频率分布表: 









 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生? 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.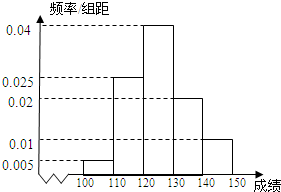 长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.