题目内容

已知下列命题中：
①终边在y轴上的角的集合是{a|a=
kπ
2
，k∈Z}；
②x=
π
8
是函数y=sin(2x+
5π
4
)的一条对称轴方程；
③函数f（x）=-x2+5x-6的零点是2，3；
④若x是锐角，则sinx+cosx＞1成立；
其中正确的命题序号为
②③④
②③④
．
分析：①当k=2时，α的终边不在y轴，可判断①错误；
②将x=
π
8
代入y=sin（2x+
5π
4
），看是否取得最值；
③解方程-x2+5x-6=0，再判断；
④利用辅助角公式将y=sinx+cosx转化为y=
2
sin（x+
π
4
），再利用正弦函数的单调性判断即可．
解答：解：对于①，当当k=2时，α=π，其终边在x轴的非正半轴，不在y轴，故①错误；
对于②，令y=f（x）=sin（2x+
5π
4
），
∵f（
π
8
）=sin（2×
π
8
+
5π
4
）=sin
3π
2
=-1，是y=f（x）的最小值，故x=
π
8
是函数y=sin（2x+
5π
4
）的一条对称轴方程，即②正确；
对于③，解方程-x2+5x-6=0得：x=2或x=3，
∴函数f（x）=-x2+5x-6的零点是2，3，正确；
对于④，令y=sinx+cosx，则y=
2
（
2
2
sinx+
2
2
cosx）=
2
sin（x+
π
4
），
∵x是锐角，即0＜x＜
π
2
，
∴x+
π
4
∈（
π
4
，
3π
4
），
∴
2
2
＜sin（x+
π
4
）≤1，
∴1＜
2
sin（x+
π
4
）≤
2
，故④正确；
综上所述，正确的命题序号为②③④．
故答案为：②③④．
点评：本题考查命题的真假判断与应用，着重考查三角函数的图象与性质，属于中档题．
练习册系列答案
相关题目
已知下列四个命题：
（1）已知扇形的面积为24π，弧长为8π，则该扇形的圆心角为
4π
3
；
（2）若θ是第二象限角，则
cos
θ
2
sin
θ
2
＜0；
（3）在平面直角坐标系中，角α的终边在直线3x+4y=0上，则tanα=-
3
4
；
（4）满足sinθ＞
1
2
的角θ取值范围是（
π
6
+2kπ，
5π
6
+2kπ），（k∈Z）
其中正确命题的序号为
（1），（3），（4）．
（1），（3），（4）．
．
下列四个命题：
（1）在四边形ABCD中，若|
AB
+
AC
|=|
AB
-
AC
|，则四边形ABCD是矩形；
（2）已知角α的终边经过点（-3a，4a）（a≠0），则sinα=
4
5
；
（3）在△ABC中，tanAtanB＜1，则△ABC的形状一定为钝角三角形；
（4）sin（α+β）≤sinα+sinβ．
其中正确的有
 
（请填写相应的序号）．
已知下列四个命题：
（1）已知扇形的面积为24π，弧长为8π，则该扇形的圆心角为；
（2）若θ是第二象限角，则＜0；
（3）在平面直角坐标系中，角α的终边在直线3x+4y=0上，则tanα=-；
（4）满足sinθ＞的角θ取值范围是（+2kπ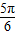，+2kπ），（k∈Z）
其中正确命题的序号为    ．

已知下列四个命题：

（1）已知扇形的面积为，弧长为，则该扇形的圆心角为；

（2）若是第二象限角，则；

（3）在平面直角坐标系中，角的终边在直线上，则；

(4) 的角取值范围是

其中正确命题的序号为        ****           。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网