题目内容
已知函数 (
( 是自然对数的底数).
是自然对数的底数).
(1)若曲线 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值;
(2)当 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与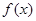 在
在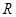 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
(1) 或
或 ;(2)
;(2) .
.
解析试题分析:(1)对 在
在 处求导,求出切线方程,与抛物线方程联立,根据
处求导,求出切线方程,与抛物线方程联立,根据 可求解;(2)求导解出
可求解;(2)求导解出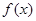 的最小值为1,对曲线C求导,令导函数为1,得到方程
的最小值为1,对曲线C求导,令导函数为1,得到方程 ,构造新函数
,构造新函数 ,用求导方法判断其零点个数,得解.
,用求导方法判断其零点个数,得解.
试题解析:(1) , 1分
, 1分
所以在 处的切线为
处的切线为
即: 2分
2分
与 联立,消去
联立,消去 得
得 ,
,
由 知,
知, 或
或 . 4分
. 4分
(2)当 时,令
时,令 得
得
则







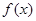
单调递减 极小值 
单调递增  6分
6分
设 ,
,
则 , 7分
, 7分
假设存在实数

练习册系列答案
相关题目
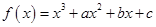 ,曲线
,曲线 在点
在点 处的切线是
处的切线是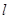 :
:
 ,
,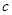 的值;
的值; 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围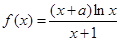 ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直. 的值;
的值;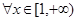 ,
,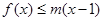 恒成立,求
恒成立,求 的范围.
的范围.
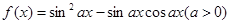 的图象与直线
的图象与直线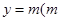 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为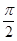
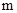 的值;
的值;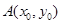 是
是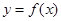 图象的对称中心,且
图象的对称中心,且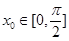 ,求点A的坐标
,求点A的坐标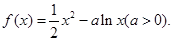
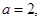 求
求 在
在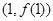 处的切线方程;
处的切线方程; 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围. =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线 .
. ,
, ,
, ,
, 的值;
的值; ≥-2时,
≥-2时, ≤
≤ ,求
,求 的取值范围.
的取值范围. (
( 为常数).
为常数).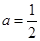 时,求
时,求 的单调递减区间;
的单调递减区间; ,且对任意的
,且对任意的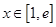 ,
, 恒成立,求实数
恒成立,求实数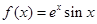 .
.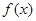 的单调区间;
的单调区间;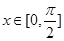 ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;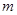 ,使得:当
,使得:当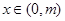 时,不等式
时,不等式 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由. ,
,
 ,求函数
,求函数 的极值;
的极值; ,求函数
,求函数 的单调区间;
的单调区间; (
( )上存在一点
)上存在一点 ,使得
,使得

 成立,求
成立,求 的取值范围.
的取值范围.