题目内容
已知函数f(x)=lnx﹣ax2+(2﹣a)x.
(I)讨论f(x)的单调性;
(II)设a>0,证明:当0<x< 时,f(
时,f( +x)>f(
+x)>f( ﹣x);
﹣x);
(III)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f'( x0)<0.
(I)讨论f(x)的单调性;
(II)设a>0,证明:当0<x<
 时,f(
时,f( +x)>f(
+x)>f( ﹣x);
﹣x);(III)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f'( x0)<0.
解:(I)函数f(x)的定义域为(0,+∞),
f'(x)=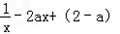 =﹣
=﹣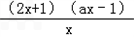 ,
,
①若a>0,则由f'(x)=0,得x= ,且当x∈(0,
,且当x∈(0, )时,f'(x)>0,
)时,f'(x)>0,
当x∈( ,+∞)时,f'(x)<0,所以f(x)在(0,
,+∞)时,f'(x)<0,所以f(x)在(0, )单调递增,在(
)单调递增,在( ,+∞)上单调递减;
,+∞)上单调递减;
②当a≤0时,f(x)>0恒 成立,因此f(x)在(0,+∞)单调递增;
(II)设函数g(x)=f( +x)﹣f(
+x)﹣f( ﹣x),则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,
﹣x),则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,
g'(x)=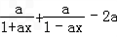 =
=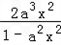 ,
,
当x∈(0, )时,g'(x)>0,而g(0)=0,所以g(x)>0,
)时,g'(x)>0,而g(0)=0,所以g(x)>0,
故当0<x< 时,f(
时,f( +x)>f(
+x)>f( ﹣x);
﹣x);
(III)由(I)可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,
故a>0,从而f(x)的最大值为f( ),且f(
),且f( )>0,
)>0,
不妨设A(x1,0),B(x2,0),0<x1<x2,则0<x1< <x2,
<x2,
由(II)得,f( ﹣x1)=f(
﹣x1)=f(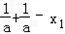 )>f(x1)=f(x2)=0,又f(x)在(
)>f(x1)=f(x2)=0,又f(x)在( ,+∞)单调递减,
,+∞)单调递减,
∴ ﹣x1<x2,于是x0=
﹣x1<x2,于是x0=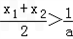 ,
,
由(I)知,f'( x0)<0.
f'(x)=
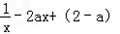 =﹣
=﹣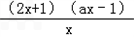 ,
,①若a>0,则由f'(x)=0,得x=
 ,且当x∈(0,
,且当x∈(0, )时,f'(x)>0,
)时,f'(x)>0,当x∈(
 ,+∞)时,f'(x)<0,所以f(x)在(0,
,+∞)时,f'(x)<0,所以f(x)在(0, )单调递增,在(
)单调递增,在( ,+∞)上单调递减;
,+∞)上单调递减;②当a≤0时,f(x)>0恒 成立,因此f(x)在(0,+∞)单调递增;
(II)设函数g(x)=f(
 +x)﹣f(
+x)﹣f( ﹣x),则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,
﹣x),则g(x)=ln(1+ax)﹣ln(1﹣ax)﹣2ax,g'(x)=
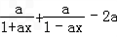 =
=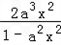 ,
,当x∈(0,
 )时,g'(x)>0,而g(0)=0,所以g(x)>0,
)时,g'(x)>0,而g(0)=0,所以g(x)>0,故当0<x<
 时,f(
时,f( +x)>f(
+x)>f( ﹣x);
﹣x);(III)由(I)可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,
故a>0,从而f(x)的最大值为f(
 ),且f(
),且f( )>0,
)>0,不妨设A(x1,0),B(x2,0),0<x1<x2,则0<x1<
 <x2,
<x2,由(II)得,f(
 ﹣x1)=f(
﹣x1)=f(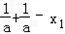 )>f(x1)=f(x2)=0,又f(x)在(
)>f(x1)=f(x2)=0,又f(x)在( ,+∞)单调递减,
,+∞)单调递减,∴
 ﹣x1<x2,于是x0=
﹣x1<x2,于是x0=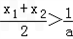 ,
,由(I)知,f'( x0)<0.

练习册系列答案
相关题目