Question

已知圆M的方程为x²+（y-2）²=1，直线l的方程为x-2y=0，点P在直线l上，过点P作圆M的切线PA，PB，切点为A，B．
（1）若∠APB=60°，试求点P的坐标；
（2）若P点的坐标为（2，1），过P作直线与圆M交于C，D两点，当CD=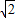时，求直线CD的方程．

Answer 1

【答案】分析：（1）设P（2m，m），代入圆方程，解得m，进而可知点P的坐标．
（2）设直线CD的斜率为k，由P的坐标表示出直线CD的解析式，利用垂径定理及勾股定理求出圆心到直线CD的距离d，利用点到直线的距离公式列出关于k的方程，求出方程的解得到k的值，即可求出直线CD的方程．
解答：解：（1）设P（2m，m），由题可知：MP==2，即（2m）²+（m-2）²=4，
解得：m=0或m=，
则P的坐标为（0，0）或（，）；
（2）设直线CD的斜率为k，由P（2，1），得到直线CD的解析式为y-1=k（x-2），即kx-y+1-2k=0，
∵圆的半径r=1，CD=，
∴圆心到直线CD的距离d==，即=，
解得：k=-或k=-1，
则直线CD的解析式为x+7y-9=0或x+y-3=0．
点评：此题考查了直线与圆的位置关系，涉及的知识有：锐角三角函数定义，两点间的距离公式，点到直线的距离公式，垂径定理，勾股定理，以及直线的点斜式方程，是一道综合性较强的试题．