题目内容
(本小题满分14分)
已知数列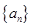 的前
的前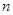 项和
项和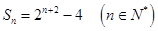 ,函数
,函数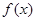 对
对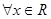 有
有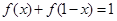 ,数列
,数列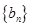 满足
满足
 .
.
(1)分别求数列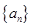 、
、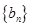 的通项公式;
的通项公式;
(2)若数列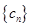 满足
满足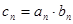 ,
,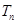 是数列
是数列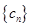 的前
的前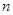 项和,若存在正实数
项和,若存在正实数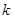 ,使不等式
,使不等式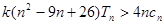 对于一切的
对于一切的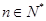 恒成立,求
恒成立,求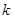 的取值范围.
的取值范围.
(1) ,
, (2)
(2)
【解析】
试题分析:(1)由题意知当 , ……1分
, ……1分
 ,
,
 时满足上式,故
时满足上式,故 , ……2分
, ……2分
∵ =1∴
=1∴ , ……3分
, ……3分
∵
 ①
①
∴
 ②
②
∴①+②,得 , ……5分
, ……5分
(2)∵ ,∴
,∴ , ……6分
, ……6分
∴ , ①
, ①
 , ②
, ②
①-②得 , ……8分
, ……8分
整理得 , ……9分
, ……9分
要使得不等式 恒成立,
恒成立,
 恒成立,
恒成立,
 对于一切的
对于一切的 恒成立,
恒成立,
即 , ……11分
, ……11分
令 ,则
,则
 ,
,
当且仅当 时等号成立,故
时等号成立,故 , ……13分
, ……13分
所以 为所求. ……14分
为所求. ……14分
考点:本小题主要考查由数列的递推公式求数列的通项公式、倒序相加法的应用和错位相减法求和的应用以及基本不等式的应用和恒成立问题的求解,考查学生综合分析问题、解决问题的能力和运算求解能力以及转化问题的能力.
点评:由数列的递推公式求通项公式时,不要忘记验证 倒序相加、错位相减、裂项相消是求和的常用常考的方法,要牢固掌握,灵活应用.
倒序相加、错位相减、裂项相消是求和的常用常考的方法,要牢固掌握,灵活应用.

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)