题目内容
设f(x)=ex-1.当a>ln 2-1且x>0时,证明:f(x)>x2-2ax.
证明:欲证f(x) >x2-2ax,即ex-1 >x2-2ax,
也就是ex-x2+2ax-1>0.
可令u(x)=ex-x2+2ax-1,则u′(x)=ex-2x+2a.
令h(x)=ex-2x+2a,则h′(x)=ex-2.
当x∈(-∞,ln 2)时,h′(x)<0,函数h(x)在(-∞,ln 2]上单调递减,当x∈(ln 2,+∞)时,h′(x)>0,函数h(x)在[ln 2,+∞)上单调递增.
所以h(x)的最小值为h(ln 2)=eln 2-2ln 2+2a
=2-2ln 2+2a.
因为a>ln 2-1,所以h(ln 2) >2-2ln 2+2(ln 2-1)=0,即h(ln 2)>0.
所以u′(x)=h(x)>0,即u(x)在R上为增函数.
故u(x)在(0,+∞)上为增函数.所以u(x)>u(0).
而u(0)=0,所以u(x)=ex-x2+2ax-1>0.
即当a>ln 2-1且x>0时,f(x)>x2-2ax.

练习册系列答案
相关题目
 平分双曲线
平分双曲线 的一条弦,则这条弦所在的直线方程为 _________
的一条弦,则这条弦所在的直线方程为 _________ 
 是纯虚数,则实数
是纯虚数,则实数 的值为_______
的值为_______ 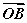 |·
|·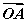 +|
+|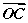 =
= ,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.
,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.



 若有
若有 则
则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 是双曲线
是双曲线 的两个焦点,
的两个焦点,  是
是 上一点,若
上一点,若 且
且 的最小内角为
的最小内角为 ,则
,则 B.
B. C.
C. D.
D.
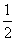 <2x<2},B={x|lgx>-1},则A∪B=( )
<2x<2},B={x|lgx>-1},则A∪B=( )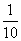 } D.{x|-1<x<10或x>10}
} D.{x|-1<x<10或x>10}