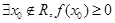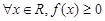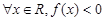题目内容
(本题满分12分)已知 :对任意
:对任意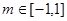 ,不等式
,不等式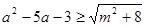 恒成立;
恒成立; :存在
:存在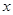 ,使不等式
,使不等式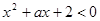 成立,若“
成立,若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数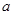 的取值范围.
的取值范围.
 :对任意
:对任意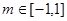 ,不等式
,不等式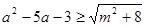 恒成立;
恒成立; :存在
:存在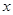 ,使不等式
,使不等式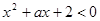 成立,若“
成立,若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数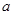 的取值范围.
的取值范围.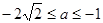 或
或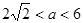
先求出p真,q真的a对应的取值范围,然后再根据“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,可得p真q假或p假q真,再分别求出a的取值范围,最后求出其并集即可.
”为假,可得p真q假或p假q真,再分别求出a的取值范围,最后求出其并集即可.
若 成立,由
成立,由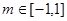 得
得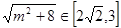
即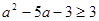 ,解得
,解得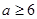 或
或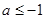 ;
;
若 成立,则不等式中
成立,则不等式中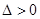 ,解得
,解得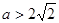 或
或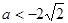 ;
;
若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,则命题
”为假,则命题 与
与 一真一假,
一真一假,
(1)若 真
真 假,则
假,则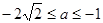 ;
;
(2)若 假
假 真,则
真,则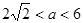 ;
;
综上: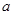 的取值范围是
的取值范围是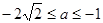 或
或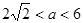
 或
或 ”为真,“
”为真,“ 且
且 ”为假,可得p真q假或p假q真,再分别求出a的取值范围,最后求出其并集即可.
”为假,可得p真q假或p假q真,再分别求出a的取值范围,最后求出其并集即可.若
 成立,由
成立,由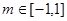 得
得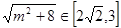
即
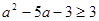 ,解得
,解得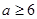 或
或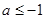 ;
;若
 成立,则不等式中
成立,则不等式中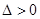 ,解得
,解得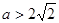 或
或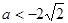 ;
;若“
 或
或 ”为真,“
”为真,“ 且
且 ”为假,则命题
”为假,则命题 与
与 一真一假,
一真一假,(1)若
 真
真 假,则
假,则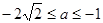 ;
;(2)若
 假
假 真,则
真,则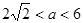 ;
;综上:
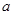 的取值范围是
的取值范围是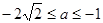 或
或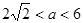

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
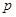 :
: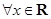 ,
,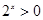 ,那么命题
,那么命题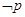 为( )
为( )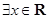 ,
,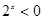
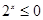
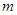 、
、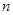 为两条不重合的直线,
为两条不重合的直线,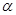 、
、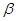 为两个不重合的平面,给出下列命题
为两个不重合的平面,给出下列命题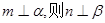 ;④
;④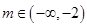 是方程
是方程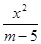 +
+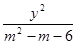 =1表示的图形为双曲线的( )
=1表示的图形为双曲线的( )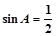 则
则
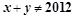 是
是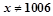 或
或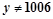 的充分不必要条件
的充分不必要条件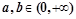 当
当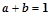 时
时
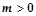 则
则 有实根
有实根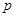 :关于
:关于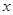 的不等式
的不等式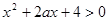 ,对一切
,对一切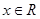 恒成立,命题
恒成立,命题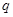 :函数
:函数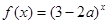 是增函数,若
是增函数,若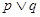 为真,
为真,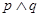 为假,求实数
为假,求实数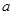 的取值范围.
的取值范围.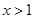 ”是“
”是“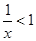 ”的( )
”的( )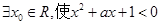 ”的否定是( )
”的否定是( )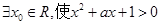
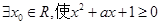
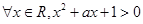 成立
成立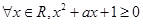 成立
成立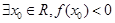 ”的否定是()
”的否定是()