Question

（本小题满分12分）

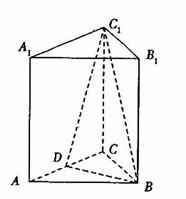
       三棱柱ABC—A₁B₁C₁中，面ABC，，AA₁=3，D为AC的中点。

   （1）求证：EF//平面PCD；

   （2）若。求棱锥P—EFC的体积。

Answer 1

解：（1）连接,交于点，则为的中点，为中点，∥，又平面，平面，∥平面  ——————4分

（2）面,,∥,面,

       则平面,，以为坐标原点，所在直线为轴，所在直线为轴，所在直线为轴建立空间直角坐标系，—————————————5分

       则,。

       设平面的法向量为，则。   ————————6分

       又平面的法向量为，

       二面角的余弦值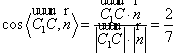，   ——————7分

       则二面角的正切值。     ————————8分

（法二）过做交于点，连接。

       面，又，

       面，则，

       则是二面角的平面角。      -------------------6分

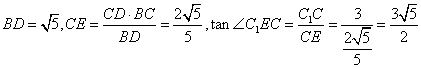       。————8分

（3）假设存在这样的点，设，则， ————————9分

       是面的法向量， ，

       则。—————————10分

       若面，则∥，即，

       此时不存在，————11分

       在侧棱上不存在点，使得面。  ——————————12分