题目内容
如题8图,在正三棱柱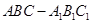 中,已知
中,已知
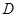 在棱
在棱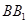 上,且
上,且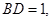 则
则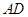 与平面
与平面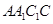 所成角的正弦值为( )
所成角的正弦值为( )
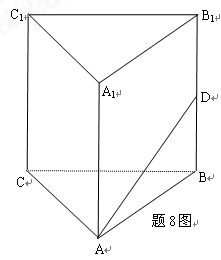
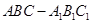 中,已知
中,已知
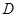 在棱
在棱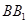 上,且
上,且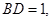 则
则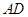 与平面
与平面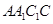 所成角的正弦值为( )
所成角的正弦值为( )
A.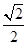 | B.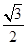 |
C.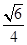 | D.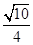 |
C
利用正三棱柱的性质找出AD在平面AA1C1C内的射影,进而得到线面角,解直角三角形求出此角的正弦值.
解答:解:如图,取C1A1、CA的中点E、F,

连接B1E与BF,则B1E⊥平面CAA1C1,
过D作DH∥B1E,则DH⊥平面CAA1C1,
连接AH,则∠DAH为所求的
DH=B1E= ,DA=
,DA= ,
,
所以sin∠DAH= ;
;
故选C.
解答:解:如图,取C1A1、CA的中点E、F,

连接B1E与BF,则B1E⊥平面CAA1C1,
过D作DH∥B1E,则DH⊥平面CAA1C1,
连接AH,则∠DAH为所求的
DH=B1E=
 ,DA=
,DA= ,
,所以sin∠DAH=
 ;
;故选C.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 中,侧面
中,侧面 与面
与面 垂直,
垂直, .
. ;
; ,求
,求 与平面
与平面 所成角的大小.
所成角的大小.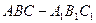 中,
中,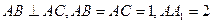 ,
,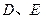 分别是
分别是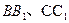 的中点,
的中点,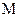 是
是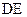 的中点.
的中点. 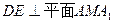 ;(2)求三棱锥
;(2)求三棱锥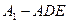 的体积;(3)求二面角
的体积;(3)求二面角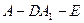 的余弦值.
的余弦值.

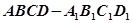 中,过顶点
中,过顶点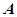 任作一条直线
任作一条直线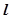 ,与异面直线
,与异面直线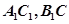
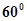 ,则这样的直线
,则这样的直线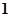 条
条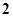 条
条 条
条 条
条 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=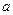 ,点E是线段SD上任意一点。
,点E是线段SD上任意一点。 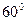 ,求线段
,求线段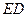 的
的 长。
长。 C所在平面,BB1=CC
C所在平面,BB1=CC 1=AC=2,
1=AC=2,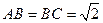 ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。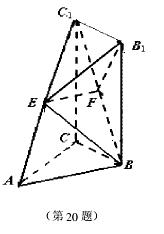 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;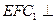 平面C1CBB1;
平面C1CBB1;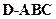 的外接球的球心O满足
的外接球的球心O满足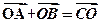 ,且外接球的体积为
,且外接球的体积为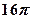 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 .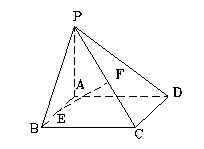 (1)求证:
(1)求证: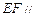 平面PAD;
平面PAD;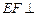 平面PCD.
平面PCD.