题目内容
已知数列{an}满足:a1=(1)求数列{an}的通项公式;
(2)证明:对于一切正整数n,不等式a1·a2·…·an<2n!恒成立.
(1)解:将条件变为1-![]() =,因此{1-
=,因此{1-![]() }为一个等比数列,其首项为1-
}为一个等比数列,其首项为1-![]() ,公比
,公比![]() ,从而1-
,从而1-![]() =
=![]() ,据此得an=
,据此得an=![]() (n≥1).①
(n≥1).①
(2)证明:据①得a1·a2·…·an= 要证a1·a1·…·an<2n!只要证n∈N*时有(1-
要证a1·a1·…·an<2n!只要证n∈N*时有(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )>
)>![]() ②
②
显然,左端每个因式都是正数,先证明,对每个n∈N*,有
(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )≥1-(
)≥1-(![]() +
+![]() +…+
+…+![]() )③
)③
用数学归纳法证明③式:a.n=1时,③式显然成立,
b.设n=k时,③式成立,
即(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )≥1-(
)≥1-(![]() +
+![]() +…+
+…+![]() ),
),
则当n=k+1时,
(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )≥〔1-(
)≥〔1-(![]() +
+![]() +…+
+…+![]() )〕(1-
)〕(1-![]() )=1-(
)=1-(![]() +
+![]() +…+
+…+![]() )-
)-![]() +
+![]() (
(![]() +
+![]() +…+
+…+![]() )≥1-(
)≥1-(![]() +
+![]() +…+
+…+![]() +
+![]() ),
),
即当n=k+1时,③式也成立。故对一切n∈N*,③式都成立。
利用③得(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )≥1-(
)≥1-(![]() +
+![]() 2+…+
2+…+![]() )=
)=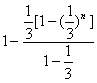 =1-
=1-![]() 〔1-(
〔1-(![]() )n〕=
)n〕=![]() +
+![]() (
(![]() )n>
)n>![]() 故②式成立,从而结论成立.
故②式成立,从而结论成立.

练习册系列答案
相关题目