题目内容
已知函数f(x)=alnx-2ax+3(a≠0).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)函数y=f(x)的图象在x=2处的切线的斜率为 ,若函数g(x)=
,若函数g(x)= ,在区间(1,3)上不是单调函数,求 m的取值范围.
,在区间(1,3)上不是单调函数,求 m的取值范围.
解:(Ⅰ)  (2分)
(2分)
当a>0时,f(x)的单调增区间为(0, ],减区间为[
],减区间为[ ,+∞);
,+∞);
当a<0时,f(x)的单调增区间为[ ,+∞),减区间为(0,
,+∞),减区间为(0, ];
];
(II)
∴a=-1
∴f(x)=-lnx+2x+3
g(x)=
=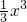 +(m+2)x2-x
+(m+2)x2-x
g'(x)=x2+2(m+2)x-1
函数g(x)= ,在区间(1,3)上不是单调函数,
,在区间(1,3)上不是单调函数,
∴g'(x)=x2+2(m+2)x-1=0在(1,3)上有解
则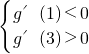 解得-
解得- <m<-2
<m<-2
∴m的取值范围为(- ,-2).
,-2).
分析:(I)利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间);
(II)对函数进行求导,令导函数等于0在区间(1,3)上有解,然后建立关系式,解之即可.
点评:本题考查利用函数的导数来求函数的单调区间,在区间(a,b)上存在极值,则在区间(a,b)上不单调,属于中档题.
 (2分)
(2分)当a>0时,f(x)的单调增区间为(0,
 ],减区间为[
],减区间为[ ,+∞);
,+∞);当a<0时,f(x)的单调增区间为[
 ,+∞),减区间为(0,
,+∞),减区间为(0, ];
];(II)

∴a=-1
∴f(x)=-lnx+2x+3
g(x)=

=
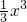 +(m+2)x2-x
+(m+2)x2-xg'(x)=x2+2(m+2)x-1
函数g(x)=
 ,在区间(1,3)上不是单调函数,
,在区间(1,3)上不是单调函数,∴g'(x)=x2+2(m+2)x-1=0在(1,3)上有解
则
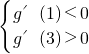 解得-
解得- <m<-2
<m<-2∴m的取值范围为(-
 ,-2).
,-2).分析:(I)利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间);
(II)对函数进行求导,令导函数等于0在区间(1,3)上有解,然后建立关系式,解之即可.
点评:本题考查利用函数的导数来求函数的单调区间,在区间(a,b)上存在极值,则在区间(a,b)上不单调,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目