题目内容
已知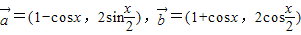
(1)若
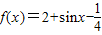 |
| -
- |2,求f(x)的表达式.
|2,求f(x)的表达式.(2)若函数f(x)和函数g(x)的图象关于原点对称,求g(x)的解析式.
(3)若h(x)=g(x)-λf(x)+1在
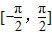 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.
【答案】分析:(1)根据 ,可求得
,可求得 =(-2cosx,2sin
=(-2cosx,2sin -2cos
-2cos ),
), =4cos2x+4-4sinx,从而可求得f(x)的表达式;
=4cos2x+4-4sinx,从而可求得f(x)的表达式;
(2)函数y=f(x)的图象上任一点M(x,y),它关于原点的对称点为N(x,y),x=-x,y=-y,利用点M在函数y=f(x)的图象上,将其坐标代入y=f(x)的表达式即可;
(3)可令t=sinx,将h(x)=g(x)-λf(x)+1在 转化为:h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1),对t2的系数-(1+λ)分类讨论,利用一次函数(λ=-1)与二次函数(λ≠-1)的性质讨论解决即可.
转化为:h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1),对t2的系数-(1+λ)分类讨论,利用一次函数(λ=-1)与二次函数(λ≠-1)的性质讨论解决即可.
解答:解(1): ,
,
=2+sinx-cos2x-1+sinx=sin2x+2sinx
(2):设函数y=f(x)的图象上任一点M(x,y)
关于原点的对称点为N(x,y)
则x=-x,y=-y,
∵点M在函数y=f(x)的图象上
∴-y=sin2(-x)+2sin(-x),即y=-sin2x+2sinx
∴函数g(x)的解析式为g(x)=-sin2x+2sinx
(3)∵h(x)=-(1+λ)sin2x+2(1-λ)sinx+1,
设sinx=t,
∵x∈
∴-1≤t≤1,
则有h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1).
①当λ=-1时,h(t)=4t+1在[-1,1]上是增函数,∴λ=-1,
②当λ≠-1时,对称轴方程为直线
ⅰ) λ<-1时, ,解得λ<-1
,解得λ<-1
ⅱ)当λ>-1时, ,解得-1<λ≤0综上,λ≤0.
,解得-1<λ≤0综上,λ≤0.
点评:本题考查三角函数的化简求值,二次函数的性质,难点在于通过三角换元得到“h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1)”后,对t2的系数-(1+λ)分类讨论,也是易错点,属于难题.
 ,可求得
,可求得 =(-2cosx,2sin
=(-2cosx,2sin -2cos
-2cos ),
), =4cos2x+4-4sinx,从而可求得f(x)的表达式;
=4cos2x+4-4sinx,从而可求得f(x)的表达式;(2)函数y=f(x)的图象上任一点M(x,y),它关于原点的对称点为N(x,y),x=-x,y=-y,利用点M在函数y=f(x)的图象上,将其坐标代入y=f(x)的表达式即可;
(3)可令t=sinx,将h(x)=g(x)-λf(x)+1在
 转化为:h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1),对t2的系数-(1+λ)分类讨论,利用一次函数(λ=-1)与二次函数(λ≠-1)的性质讨论解决即可.
转化为:h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1),对t2的系数-(1+λ)分类讨论,利用一次函数(λ=-1)与二次函数(λ≠-1)的性质讨论解决即可.解答:解(1):
 ,
,=2+sinx-cos2x-1+sinx=sin2x+2sinx
(2):设函数y=f(x)的图象上任一点M(x,y)
关于原点的对称点为N(x,y)
则x=-x,y=-y,
∵点M在函数y=f(x)的图象上
∴-y=sin2(-x)+2sin(-x),即y=-sin2x+2sinx
∴函数g(x)的解析式为g(x)=-sin2x+2sinx
(3)∵h(x)=-(1+λ)sin2x+2(1-λ)sinx+1,
设sinx=t,
∵x∈

∴-1≤t≤1,
则有h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1).
①当λ=-1时,h(t)=4t+1在[-1,1]上是增函数,∴λ=-1,
②当λ≠-1时,对称轴方程为直线

ⅰ) λ<-1时,
 ,解得λ<-1
,解得λ<-1ⅱ)当λ>-1时,
 ,解得-1<λ≤0综上,λ≤0.
,解得-1<λ≤0综上,λ≤0.点评:本题考查三角函数的化简求值,二次函数的性质,难点在于通过三角换元得到“h(t)=-(1+λ)t2+2(1-λ)t+1(-1≤t≤1)”后,对t2的系数-(1+λ)分类讨论,也是易错点,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
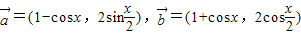
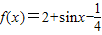 |
|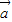 -
-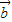 |2,求f(x)的表达式.
|2,求f(x)的表达式.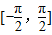 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.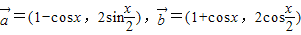
 |
|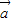 -
- |2,求f(x)的表达式.
|2,求f(x)的表达式.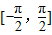 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.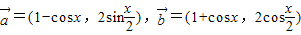
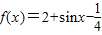 |
|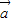 -
-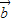 |2,求f(x)的表达式.
|2,求f(x)的表达式.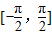 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.