题目内容
已知函数 在
在 上单调递减,则
上单调递减,则 的取值范围是
的取值范围是

解析试题分析:因为, 在
在 上单调递减,
上单调递减,
所以,
 0在(1,2)成立,
0在(1,2)成立,
即, 在(1,2)成立,而
在(1,2)成立,而 在(1,2)是增函数,所以其最大值为
在(1,2)是增函数,所以其最大值为 ,故
,故 。
。
考点:本题主要考查利用导数研究函数的单调性。
点评:中档题,求解本题的关键是利用函数的单调递减区间,得出参数所满足的不等式。转化成不等式恒成立问题,通过研究函数的最值,使问题得解。根据题设转化出不等式是本题的易错点。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 求
求 .
. (
( 为自然对数的底数),函数
为自然对数的底数),函数 ,则
,则 __________.
__________. =________.
=________. ,则
,则 为 。
为 。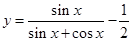 在点M(
在点M(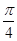 ,0)处的切线的斜率为________________.
,0)处的切线的斜率为________________. .
.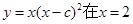 处有极大值,则常数c= ;
处有极大值,则常数c= ; ,则二项式
,则二项式 展开式中含
展开式中含 项的系数是_________.
项的系数是_________.