题目内容
已知正方体ABCD-A1B1C1D1的棱长为1,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是
- A.2
- B.

- C.
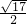
- D.

C
分析:根据题意可得:可以把平面BCC1B1展开,根据图象可得若PE+EC取最小值,则P,E,C三点共线,可得PE+EC的最小值为PC的长度,再结合题意求出答案即可.
解答:根据题意可得:可以把平面BCC1B1展开,如图所示,

若PE+EC取最小值,则P,E,C三点共线,
所以PE+EC的最小值为PC,
因为正方体ABCD-A1B1C1D1的棱长为1,P是AA1的中点,
所以|PC|=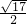 .
.
故选C.
点评:本题主要考查空间中点之间的距离,解决此题的关键是能够把空间问题转化为平面问题.
分析:根据题意可得:可以把平面BCC1B1展开,根据图象可得若PE+EC取最小值,则P,E,C三点共线,可得PE+EC的最小值为PC的长度,再结合题意求出答案即可.
解答:根据题意可得:可以把平面BCC1B1展开,如图所示,

若PE+EC取最小值,则P,E,C三点共线,
所以PE+EC的最小值为PC,
因为正方体ABCD-A1B1C1D1的棱长为1,P是AA1的中点,
所以|PC|=
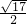 .
.故选C.
点评:本题主要考查空间中点之间的距离,解决此题的关键是能够把空间问题转化为平面问题.

练习册系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.