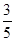题目内容
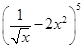 的展开式中常数项是( )
的展开式中常数项是( )
| A.5 | B.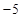 | C.10 | D. |
D
解析试题分析:常数项为: .
.
考点:二项式定理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若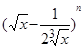 的展开式中第四项为常数项,则
的展开式中第四项为常数项,则 ( )
( )
A. | B.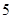 | C. | D.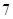 |
某学校组织演讲比赛,准备从甲、乙等8名学生中选派4名学生参加,要求甲、乙两名同学至少有一人参加,且若甲、乙同时参加时,他们的演讲顺序不能相邻,那么不同的演讲顺序的种数为( )
| A.1860 | B.1320 | C.1140 | D.1020 |
若 展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
A. | B.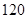 | C.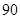 | D. |
某校周四下午第五、六两节是选修课时间,现有甲、乙、丙、丁四位教师可开课。已知甲、乙教师各自最多可以开设两节课,丙、丁教师各自最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则不同的开课方案共有( )种。
| A.20 | B.19 | C.16 | D.15 |
 的二项展开式中,
的二项展开式中, 项的系数是( )
项的系数是( )
| A.45 | B.90 | C.135 | D.270 |
我们把各位数字之和为6的四位数称为“六合数”(如2 013是“六合数”),则“六合数”中首位为2的“六合数”共有( )
| A.18个 | B.15个 |
| C.12个 | D.9个 |
有4名优秀学生A,B,C,D全部被保送到甲、乙、丙3所学校,每所学校至少去一名,且A生不去甲校,则不同的保送方案有( ).
| A.24种 | B.30种 | C.36种 | D.48种 |