题目内容
已知A,B,C是椭圆m: +
+ =1(a>b>0)上的三点,其中点A的坐标为(2
=1(a>b>0)上的三点,其中点A的坐标为(2 ,0),BC过椭圆m的中心,且
,0),BC过椭圆m的中心,且 ,且|
,且| |=2|
|=2| |.
|.(1)求椭圆m的方程;
(2)过点M(0,t)的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且|
 |=|
|=| |.求实数t的取值范围.
|.求实数t的取值范围.
【答案】分析:(1)如图, 点A是椭圆m的右顶点,∴a=2
点A是椭圆m的右顶点,∴a=2 ;由
;由 •
• =0,得AC⊥BC;由
=0,得AC⊥BC;由 =2
=2 和椭圆的对称性,得
和椭圆的对称性,得 =
= ;这样,可以得出点C的坐标,把C点的坐标代入椭圆标准方程,可求得.
;这样,可以得出点C的坐标,把C点的坐标代入椭圆标准方程,可求得.
(2)如图, 过点M的直线l,与椭圆m交于两点P,Q;当斜率k=0时,点M在椭圆内,则-2<t<2;当k≠0时,设过M点的直线l:y=kx+t与椭圆方程组成方程组,消去y,可得关于x的一元二次方程,由判别式△>0,得不等式①,由x1+x2的值可得PQ的中点H坐标,由
过点M的直线l,与椭圆m交于两点P,Q;当斜率k=0时,点M在椭圆内,则-2<t<2;当k≠0时,设过M点的直线l:y=kx+t与椭圆方程组成方程组,消去y,可得关于x的一元二次方程,由判别式△>0,得不等式①,由x1+x2的值可得PQ的中点H坐标,由 =
= ,得DH⊥PQ,所以斜率
,得DH⊥PQ,所以斜率 ,这样得等式②;
,这样得等式②;
由①②可得t的范围.
解答:解(1)如图所示,
∵ =2
=2 ,且BC过点O(0,0),则
,且BC过点O(0,0),则 ;
;
又 •
• =0,∴∠OCA=90°,且A(2
=0,∴∠OCA=90°,且A(2 ,0),则点C
,0),则点C ,
,
由a= ,可设椭圆的方程m:
,可设椭圆的方程m: ;
;
将C点坐标代入方程m,得 ,解得c2=8,b2=4;
,解得c2=8,b2=4;
∴椭圆m的方程为: ;
;
(2)如图所示,
由题意,知D(0,-2),∵M(0,t),
∴1°当k=0时,显然-2<t<2,
2°当k≠0时,设l:y=kx+t,则
 ,消去y,得(1+3k2)x2+6ktx+3t2-12=0;
,消去y,得(1+3k2)x2+6ktx+3t2-12=0;
由△>0,可得t2<4+12k2 ①
设点P(x1,y1),Q(x2,y2),且PQ的中点为H(x,y);
则x= =-
=- ,y=kx+t=
,y=kx+t= ,∴H
,∴H ;
;
由 ,∴DH⊥PQ,则kDH=-
,∴DH⊥PQ,则kDH=- ,∴
,∴ =-
=- ;
;
∴t=1+3k2 ②
∴t>1,将①代入②,得1<t<4,∴t的范围是(1,4);
综上,得t∈(-2,4).
点评:本题考查了直线与椭圆知识的综合应用,以及向量在解析几何中的应用;用数形结合的方法比较容易理清思路,解得结果.
 点A是椭圆m的右顶点,∴a=2
点A是椭圆m的右顶点,∴a=2 ;由
;由 •
• =0,得AC⊥BC;由
=0,得AC⊥BC;由 =2
=2 和椭圆的对称性,得
和椭圆的对称性,得 =
= ;这样,可以得出点C的坐标,把C点的坐标代入椭圆标准方程,可求得.
;这样,可以得出点C的坐标,把C点的坐标代入椭圆标准方程,可求得.(2)如图,
 过点M的直线l,与椭圆m交于两点P,Q;当斜率k=0时,点M在椭圆内,则-2<t<2;当k≠0时,设过M点的直线l:y=kx+t与椭圆方程组成方程组,消去y,可得关于x的一元二次方程,由判别式△>0,得不等式①,由x1+x2的值可得PQ的中点H坐标,由
过点M的直线l,与椭圆m交于两点P,Q;当斜率k=0时,点M在椭圆内,则-2<t<2;当k≠0时,设过M点的直线l:y=kx+t与椭圆方程组成方程组,消去y,可得关于x的一元二次方程,由判别式△>0,得不等式①,由x1+x2的值可得PQ的中点H坐标,由 =
= ,得DH⊥PQ,所以斜率
,得DH⊥PQ,所以斜率 ,这样得等式②;
,这样得等式②;由①②可得t的范围.
解答:解(1)如图所示,

∵
 =2
=2 ,且BC过点O(0,0),则
,且BC过点O(0,0),则 ;
;又
 •
• =0,∴∠OCA=90°,且A(2
=0,∴∠OCA=90°,且A(2 ,0),则点C
,0),则点C ,
,由a=
 ,可设椭圆的方程m:
,可设椭圆的方程m: ;
;将C点坐标代入方程m,得
 ,解得c2=8,b2=4;
,解得c2=8,b2=4;∴椭圆m的方程为:
 ;
;(2)如图所示,

由题意,知D(0,-2),∵M(0,t),
∴1°当k=0时,显然-2<t<2,
2°当k≠0时,设l:y=kx+t,则
 ,消去y,得(1+3k2)x2+6ktx+3t2-12=0;
,消去y,得(1+3k2)x2+6ktx+3t2-12=0;由△>0,可得t2<4+12k2 ①
设点P(x1,y1),Q(x2,y2),且PQ的中点为H(x,y);
则x=
 =-
=- ,y=kx+t=
,y=kx+t= ,∴H
,∴H ;
;由
 ,∴DH⊥PQ,则kDH=-
,∴DH⊥PQ,则kDH=- ,∴
,∴ =-
=- ;
;∴t=1+3k2 ②
∴t>1,将①代入②,得1<t<4,∴t的范围是(1,4);
综上,得t∈(-2,4).
点评:本题考查了直线与椭圆知识的综合应用,以及向量在解析几何中的应用;用数形结合的方法比较容易理清思路,解得结果.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
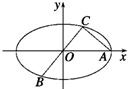 如图所示,已知A,B,C是椭圆
如图所示,已知A,B,C是椭圆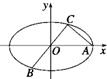 如图所示,已知A、B、C是椭圆E:
如图所示,已知A、B、C是椭圆E: