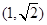题目内容
已知抛物线 的焦点
的焦点 与双曲线
与双曲线 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与 轴的交点为
轴的交点为 ,点
,点 在抛物线上且
在抛物线上且 ,则△
,则△ 的面积为
的面积为
| A.4 | B.8 | C.16 | D.32 |
D
解析试题分析:解:点A在抛物线准线上的射影为D,根据抛物线性质可知|AF|=|AD|,∵双曲线 的右焦点为(4,0),即抛物线焦点为(4,0)∴
的右焦点为(4,0),即抛物线焦点为(4,0)∴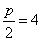 ,p=8,∵
,p=8,∵ =
=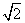 |AD|,∴∠DKA=∠AKF=45°,设A点坐标为(
|AD|,∴∠DKA=∠AKF=45°,设A点坐标为(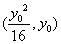 ,则有
,则有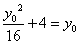 ,解得y0=8,∴|AK|=
,解得y0=8,∴|AK|=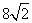 ∴△AFK的面积为
∴△AFK的面积为 •|AK|•|KF|sin45°=32,故选D
•|AK|•|KF|sin45°=32,故选D
考点:抛物线
点评:本题主要考查了抛物线的性质.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线 上一定点B(-1,0)和两个动点
上一定点B(-1,0)和两个动点 ,当
,当 时,点
时,点 的横坐标的取值范围是
的横坐标的取值范围是
A. ∪ ∪  | B. |
C. | D.(-∞,-3]∪ |
角 的终边经过点A
的终边经过点A ,且点A在抛物线
,且点A在抛物线 的准线上,则
的准线上,则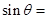 ( )
( )
A. | B. | C. | D. |
 的离心率为
的离心率为 . 双曲线
. 双曲线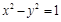 的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )



 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设 ,则
,则 等于( )
等于( ) B.
B.  C.
C. D.
D. 
 的左右焦点分别为
的左右焦点分别为 ,
, 为双曲线的离心率,P是双曲线右支上的点,
为双曲线的离心率,P是双曲线右支上的点, 的内切圆的圆心为I,过
的内切圆的圆心为I,过 作直线PI的垂线,垂足为B,则OB=
作直线PI的垂线,垂足为B,则OB=


 的右焦点为
的右焦点为 ,过点
,过点 轴垂直的直线
轴垂直的直线 交两渐近线于A,B两点,与双曲线的其中一个交点为
交两渐近线于A,B两点,与双曲线的其中一个交点为 ,设O为坐标原点,若
,设O为坐标原点,若 (
( ),且
),且 ,则该双曲线的离心率为
,则该双曲线的离心率为



 是双曲线
是双曲线 上一点,
上一点, 、
、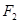 是其左、右焦点,
是其左、右焦点, 的三边长成等差数列,且
的三边长成等差数列,且 ,则双曲线的离心率等于
,则双曲线的离心率等于



 与双曲线
与双曲线 相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )