题目内容
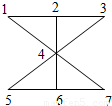
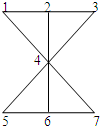 把三盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为( )
把三盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为( )分析:因为三盆兰花不能放在一条直线,所以可先放在一个三角形的三个角上,分析图中7个点可组成多少个三角形,7个点中任选3个,再去掉共线的即可,然后,任取一个三角形,放三盆兰花,剩下的位置放4盆不同的玫瑰花即可.
解答:解:7个点可组成的三角形有C73-5=30
∵三盆兰花不能放在一条直线上,∴可放入三角形三个角上,有C301A33=180中放法
再放4盆不同的玫瑰花,没有限制,放在剩余4个位置,有A44=24中放法
∴不同的摆放方法为180×24=4320种.
故选B
∵三盆兰花不能放在一条直线上,∴可放入三角形三个角上,有C301A33=180中放法
再放4盆不同的玫瑰花,没有限制,放在剩余4个位置,有A44=24中放法
∴不同的摆放方法为180×24=4320种.
故选B
点评:本题考查了有限制的排列组合问题,做题时要认真分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
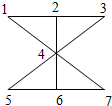 把3盆不同的兰花和4盆不同的玫瑰花摆放在如图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为
把3盆不同的兰花和4盆不同的玫瑰花摆放在如图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为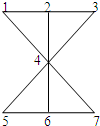 把三盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为
把三盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为