题目内容
在△ABC中,cos2| A |
| 2 |
| b+c |
| 2c |
| 9 |
| 10 |
分析:由cos2
=
=
,再由b2+a2=c2,求得a,b,c的值,再由S=
(a+b+c)•r=
ab,求得内切圆半径r,再求内切圆面积.
| A |
| 2 |
| b+c |
| 2c |
| 9 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由cos2
=
,得cosA=
,又cos2
=
,所以cosA=
,再由余弦定理得b2+a2=c2,因为c=5,所以a=3,b=4.设其内切圆的半径为r,因为S=
(a+b+c)•r=
ab,∴r=1,所以内切圆的面积是π.
故答案为:π
| A |
| 2 |
| 9 |
| 10 |
| 4 |
| 5 |
| A |
| 2 |
| b+c |
| 2c |
| b |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:π
点评:本题考查了余弦定理的应用以及三角形面积与内切圆半径和周长的关系,是中档题.

练习册系列答案
相关题目
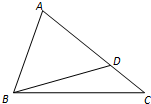 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=