题目内容
数列{an}中,a1=1,当n≥2时,an是 的二项展开式中x的系数,设
的二项展开式中x的系数,设 为数列{bn}的前n项和,则an=________,T99=________.
为数列{bn}的前n项和,则an=________,T99=________.


分析:利用
 的二项展开式的通项公式可求得二项展开式中x的系数,即当n≥2时的an,
的二项展开式的通项公式可求得二项展开式中x的系数,即当n≥2时的an,解答:设
 的二项展开式的通项公式为Tr+1=
的二项展开式的通项公式为Tr+1= (-1)r•3n-r•
(-1)r•3n-r• ,
,令r=2,则T3=
 3n-2x,
3n-2x,∴当n≥2时,an=
 •3n-2,
•3n-2,∴an=

又bn=
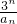 ,数列{bn}的前n项和为Tn,
,数列{bn}的前n项和为Tn,∴当n≥2时,bn=
 =
=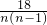 =18(
=18( -
- ),又b1=3,
),又b1=3,∴T99=3+18[(1-
 )+(
)+( -
- )+…+(
)+…+( -
- )]
)]=3+18(1-
 )
)=3+

=
 .
.故答案为:
 ;
; .
.点评:本题考查二项式定理,考查数列的裂项法求和,考查分类讨论思想与化归思想的综合应用,属于难题.

练习册系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|