题目内容
如图 E，F，G，H分别是四边形ABCD的所在边的中点，若
，则四边形EFGH是
- A.平行四边形，但不是矩形也不是菱形
- B.矩形
- C.菱形
- D.正方形
B
分析：利用E，F，G，H分别是四边形ABCD的所在边的中点，确定四边形EFGH是平行四边形，利用
，可得
，从而EF⊥FG，即可判断四边形EFGH是矩形．
解答：
解：连接AC，BD
∵E，F，G，H分别是四边形ABCD的所在边的中点，
∴EF∥GH∥AC，EF=GH=
AC
∴四边形EFGH是平行四边形
∵
∴
∴
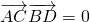
∴AC⊥BD
∵EF∥AC，FG∥BD
∴EF⊥FG
∴四边形EFGH是矩形
故选B．
点评：本题考查向量知识的运用，考查平行性的传递性，解题的关键是确定四边形为平行四边形及邻边垂直．
分析：利用E，F，G，H分别是四边形ABCD的所在边的中点，确定四边形EFGH是平行四边形，利用
，可得，从而EF⊥FG，即可判断四边形EFGH是矩形．解答：
解：连接AC，BD∵E，F，G，H分别是四边形ABCD的所在边的中点，
∴EF∥GH∥AC，EF=GH=
AC∴四边形EFGH是平行四边形
∵
∴
∴
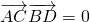
∴AC⊥BD
∵EF∥AC，FG∥BD
∴EF⊥FG
∴四边形EFGH是矩形
故选B．
点评：本题考查向量知识的运用，考查平行性的传递性，解题的关键是确定四边形为平行四边形及邻边垂直．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图 E，F，G，H分别是四边形ABCD的所在边的中点，若
某市为加强城市圈的建设，计划对周边如图所示的A、B、C、D、E、F、G、H八个中小城市进行综合规划治理，第一期工程拟从这八个中小城市中选取三个城市，但要求没有任何两个城市相邻，则城市A被选中的概率为
