题目内容
以下四个命题:
①在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=acosB,则B=
;
②设
,
是两个非零向量且|
•
|=|
||
|,则存在实数λ,使得
=λ
;
③方程sinx-x=0在实数范围内的解有且仅有一个;
④a,b∈R且a3-3b>b3-3a,则a>b;
其中正确的是
①在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=acosB,则B=
| π |
| 4 |
②设
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
③方程sinx-x=0在实数范围内的解有且仅有一个;
④a,b∈R且a3-3b>b3-3a,则a>b;
其中正确的是
①②③④
①②③④
.分析:分别根据条件判别各命题的真假即可.①利用正弦定理化简求角.②由|
•
|=|
||
|得出向量的夹角,根据夹角判断是否共线.③构造函数y=sinx-x,利用导数判断函数是单调的即可.④利用作差法进行判断.
| a |
| b |
| a |
| b |
解答:解:①在三角形中,根据正弦定理可知bsinA=acosB等价为sinAsinB=sinAcosB,所以sinB=cosB,即B=
,所以正确.
②由|
•
|=|
||
|,得|cos<
,
>|=1,所以
,
的夹角为0或π,所以
,
共线,所以存在实数λ,使得
=λ
,所以正确.
③设y=sinx-x,则y'=cosx-1≤0,所以函数y=sinx-x在定义域上单调递减.因为f(0)=0,所以方程sinx-x=0在实数范围内的解有且仅有一个,所以正确.
④因为a3-b3+3a-3b=(a-b)(a2+ab+b2+3)=(a-b)[(a+
b)2+
b2+3],所以若a3-3b>b3-3a,则必有a>b成立,所以正确.
故答案为:①②③④.
| π |
| 4 |
②由|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
③设y=sinx-x,则y'=cosx-1≤0,所以函数y=sinx-x在定义域上单调递减.因为f(0)=0,所以方程sinx-x=0在实数范围内的解有且仅有一个,所以正确.
④因为a3-b3+3a-3b=(a-b)(a2+ab+b2+3)=(a-b)[(a+
| 1 |
| 2 |
| 3 |
| 4 |
故答案为:①②③④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
 中, “
中, “ ”是“
”是“ ”的必要而非充分条件;
”的必要而非充分条件; 的最小正周期是
的最小正周期是 ;
;

 ,则
,则 与函数
与函数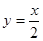 的图象有三个交点
的图象有三个交点 B.
2 C.
3
D. 4
B.
2 C.
3
D. 4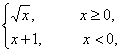 则
则