题目内容
6．复数z满足（-1+i）z=（1+i）2，其中i为虚数单位，则在复平面上复数z的共轭复数$\overline z$对应的点位于第一象限．分析 根据复数的基本运算和复数的几何意义，进行判断即可．
解答 解：∵（-1+i）z=（1+i）2=2i，
则z=$\frac{2i}{-1+i}$=$\frac{2i（-1-i）}{（-1+i）（-1-i）}$=$\frac{-2i+2}{2}$=1-i，
则$\overline z$=1+i，对应的坐标为（1，1），位于第一象限，
故答案为：一．
点评 本题主要考查复数的几何意义，利用复数的基本运算是解决本题的关键．
练习册系列答案
相关题目
16．有10件产品，其中有2件次品，每次抽取1件检验，抽检后不放回，共抽2次，则第1次抽到正品，第2次抽到次品的概率是（ ）
| A． | $\frac{32}{45}$ | B． | $\frac{16}{45}$ | C． | $\frac{8}{45}$ | D． | $\frac{4}{45}$ |
18．函数y=x-sinx，x∈[$\frac{π}{2}$，π]的最大值是（ ）
| A． | $\frac{π}{2}-1$ | B． | π-1 | C． | π | D． | π+1 |
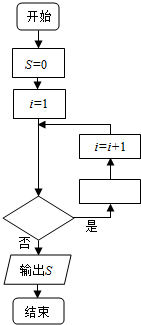如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图．