题目内容
已知函数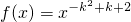 ,且f(2)<f(3),则实数k取值范围是______.
,且f(2)<f(3),则实数k取值范围是______.
解:因为函数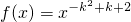 是幂函数,且f(2)<f(3),
是幂函数,且f(2)<f(3),
所以其在(0,+∞)上是增函数,
所以根据幂函数的性质,有-k2+k+2>0,即k2-k-2<0,
所以-1<k<2.
故答案为(-1,2).
分析:由于给出的函数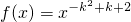 是幂函数,且f(2)<f(3),所以其在(0,+∞)上是增函数,其指数为正,求解一元二次方程得k取值范围.
是幂函数,且f(2)<f(3),所以其在(0,+∞)上是增函数,其指数为正,求解一元二次方程得k取值范围.
点评:本题考查了幂函数的概念,解答的关键是熟记幂函数的定义及性质,此题是基础题.
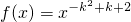 是幂函数,且f(2)<f(3),
是幂函数,且f(2)<f(3),所以其在(0,+∞)上是增函数,
所以根据幂函数的性质,有-k2+k+2>0,即k2-k-2<0,
所以-1<k<2.
故答案为(-1,2).
分析:由于给出的函数
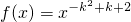 是幂函数,且f(2)<f(3),所以其在(0,+∞)上是增函数,其指数为正,求解一元二次方程得k取值范围.
是幂函数,且f(2)<f(3),所以其在(0,+∞)上是增函数,其指数为正,求解一元二次方程得k取值范围.点评:本题考查了幂函数的概念,解答的关键是熟记幂函数的定义及性质,此题是基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
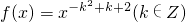 ,且f(2)<f(3)
,且f(2)<f(3)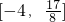 .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由.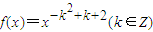 ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由.