题目内容
过抛物线y2=4x的焦点F作弦AB,若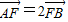 ,则弦AB所在直线的方程是 _.
,则弦AB所在直线的方程是 _.
【答案】分析:设出直线方程,把直线方程和抛物线方程联立后得到关于x的一元二次方程,利用根与系数关系得到两个交点的横坐标的和与积,由 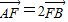 ,代入坐标整理后得到直线的斜率与截距间的关系,由两个向量的模相等,结合抛物线定义可求出两个交点横坐标的具体值,代入两根和的关系式得到直线的斜率与截距的另一关系式,解方程组可求解k的值.
,代入坐标整理后得到直线的斜率与截距间的关系,由两个向量的模相等,结合抛物线定义可求出两个交点横坐标的具体值,代入两根和的关系式得到直线的斜率与截距的另一关系式,解方程组可求解k的值.
解答:解:设直线l的方程为y=kx+m(k≠0),与抛物线y2=4x相交于A(x1,y1),B(x2,y2).
联立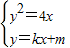 ,得k2x2+(2km-4)x+m2=0.
,得k2x2+(2km-4)x+m2=0.
所以△=(2km-4)2-4k2m2=16-16km>0,即km<1.
x1+x2=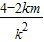 ,x1x2=
,x1x2=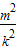 .
.
由y2=4x得其焦点F(1,0).
由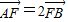 ,得(1-x1,-y1)=2(x2-1,y2).
,得(1-x1,-y1)=2(x2-1,y2).
所以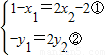 ,
,
由①得,x1+2x2=3 ③
由②得,x1+2x2=-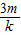 .
.
所以m=-k.
再由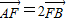 ,得|
,得|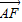 |=2|
|=2|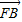 |,
|,
所以x1+1=2(x2+1),即x1-2x2=1④
联立③④得x1=2,x2= .
.
所以x1+x2=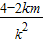 =
= .
.
把m=-k代入得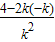 =
= ,解得|k|=2
,解得|k|=2 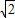 ,满足mk=-8<1.
,满足mk=-8<1.
所以k=±2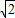 .
.
则弦AB所在直线的方程是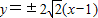 .
.
故答案为: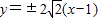 .
.
点评:本题考查了抛物线的简单几何性质,考查了直线与圆锥曲线的关系,解答的关键是利用向量关系得到两个交点A,B的坐标的关系,同时灵活运用了抛物线的定义,属中高档题.
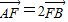 ,代入坐标整理后得到直线的斜率与截距间的关系,由两个向量的模相等,结合抛物线定义可求出两个交点横坐标的具体值,代入两根和的关系式得到直线的斜率与截距的另一关系式,解方程组可求解k的值.
,代入坐标整理后得到直线的斜率与截距间的关系,由两个向量的模相等,结合抛物线定义可求出两个交点横坐标的具体值,代入两根和的关系式得到直线的斜率与截距的另一关系式,解方程组可求解k的值.解答:解:设直线l的方程为y=kx+m(k≠0),与抛物线y2=4x相交于A(x1,y1),B(x2,y2).
联立
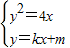 ,得k2x2+(2km-4)x+m2=0.
,得k2x2+(2km-4)x+m2=0.所以△=(2km-4)2-4k2m2=16-16km>0,即km<1.
x1+x2=
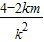 ,x1x2=
,x1x2=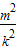 .
.由y2=4x得其焦点F(1,0).
由
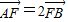 ,得(1-x1,-y1)=2(x2-1,y2).
,得(1-x1,-y1)=2(x2-1,y2).所以
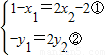 ,
,由①得,x1+2x2=3 ③
由②得,x1+2x2=-
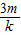 .
.所以m=-k.
再由
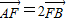 ,得|
,得|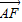 |=2|
|=2|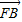 |,
|,所以x1+1=2(x2+1),即x1-2x2=1④
联立③④得x1=2,x2=
 .
.所以x1+x2=
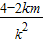 =
= .
.把m=-k代入得
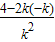 =
= ,解得|k|=2
,解得|k|=2 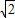 ,满足mk=-8<1.
,满足mk=-8<1.所以k=±2
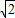 .
.则弦AB所在直线的方程是
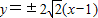 .
.故答案为:
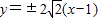 .
.点评:本题考查了抛物线的简单几何性质,考查了直线与圆锥曲线的关系,解答的关键是利用向量关系得到两个交点A,B的坐标的关系,同时灵活运用了抛物线的定义,属中高档题.

练习册系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A,B两点,则|AB|=( )
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|