题目内容
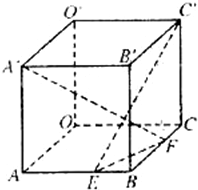
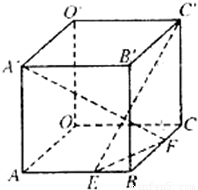 在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.
在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.(Ⅰ)求证:A′F⊥C′E;
(Ⅱ)当三棱锥B′-BEF的体积取得最大值时,求二面角B′-EF-B的大小.(结果用反三角函数表示)
【答案】分析:(I)以O为原点建立空间直角坐标系,AE=BF=x,验证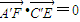 ,即可证明A′F⊥C′E;
,即可证明A′F⊥C′E;
(Ⅱ)利用基本不等式,确定三棱锥B′-BEF的体积取得最大值时,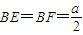 ,过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF,从而∠B′DB是二面角B′-EF-B的平面角,即可求出二面角B′-EF-B的大小.
,过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF,从而∠B′DB是二面角B′-EF-B的平面角,即可求出二面角B′-EF-B的大小.
解答: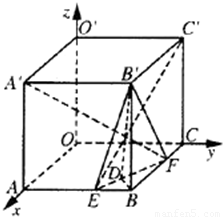 (I)证明:如图,以O为原点建立空间直角坐标系.
(I)证明:如图,以O为原点建立空间直角坐标系.
设AE=BF=x,则A′(a,0,a)、F(a-x,a,0)、C′(0,a,a)、E(a,x,0)
∴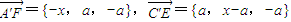 .…(4分)
.…(4分)
∵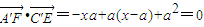 ,
,
∴A′F⊥C′E.
(II)解:记BF=x,BE=y,则x+y=a,
三棱锥B′-BEF的体积 ,
,
当且仅当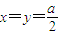 时,等号成立.
时,等号成立.
因此,三棱锥B′-BEF的体积取得最大值时,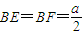 .…(10分)
.…(10分)
过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF.
∴∠B′DB是二面角B′-EF-B的平面角.
在直角三角形BEF中,直角边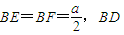 是斜边上的高,
是斜边上的高,
∴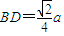 ,
,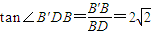 ,
,
故二面角B′-EF-B的大小为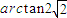 .…(14分)
.…(14分)
点评:本题考查线线垂直,考查面面角,考查向量知识的运用,考查三棱锥的体积,考查基本不等式的运用,属于中档题.
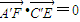 ,即可证明A′F⊥C′E;
,即可证明A′F⊥C′E;(Ⅱ)利用基本不等式,确定三棱锥B′-BEF的体积取得最大值时,
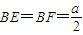 ,过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF,从而∠B′DB是二面角B′-EF-B的平面角,即可求出二面角B′-EF-B的大小.
,过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF,从而∠B′DB是二面角B′-EF-B的平面角,即可求出二面角B′-EF-B的大小.解答:
 (I)证明:如图,以O为原点建立空间直角坐标系.
(I)证明:如图,以O为原点建立空间直角坐标系.设AE=BF=x,则A′(a,0,a)、F(a-x,a,0)、C′(0,a,a)、E(a,x,0)
∴
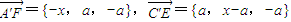 .…(4分)
.…(4分)∵
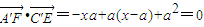 ,
,∴A′F⊥C′E.
(II)解:记BF=x,BE=y,则x+y=a,
三棱锥B′-BEF的体积
 ,
,当且仅当
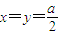 时,等号成立.
时,等号成立.因此,三棱锥B′-BEF的体积取得最大值时,
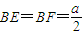 .…(10分)
.…(10分)过B作BD⊥EF交EF于D,连B′D,可知B′D⊥EF.
∴∠B′DB是二面角B′-EF-B的平面角.
在直角三角形BEF中,直角边
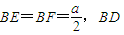 是斜边上的高,
是斜边上的高,∴
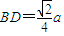 ,
,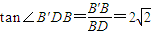 ,
,故二面角B′-EF-B的大小为
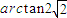 .…(14分)
.…(14分)点评:本题考查线线垂直,考查面面角,考查向量知识的运用,考查三棱锥的体积,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=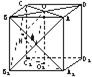 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、O、O1分别是A1B、AC、A1C1的中点,且OH⊥O1B,垂足为H.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、O、O1分别是A1B、AC、A1C1的中点,且OH⊥O1B,垂足为H.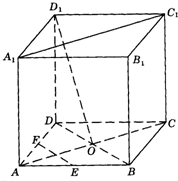 如图,在棱长为a的正方体ABCD-A1B1C1D1中,O是AC、BD的交点,E,F分别是AB与AD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,O是AC、BD的交点,E,F分别是AB与AD的中点. (2001•上海)在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.
(2001•上海)在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.