题目内容
已知f(x)=x3+ax2+bx+c有极大值f(a)和极小值f(b)。
(1)求f(a)+f(b);
(2)设曲线y=f(x)的极值点为A、B,求证:A、B连线的中点M在y=f(x)上。
答案:
解析:
解析:
解:∵ f(x)=x3+ax2+bx+c,∴ f′(x)=3x3+2ax+b, 令f′(x)=0,得3x3+2ax+b=0。 ∵ a、b是方程3x3+2ax+b=0的两个根,∴ a+b=- (1)f(a)+f(b)=a3+aa2+ba+c+b3+a b2+bb+c =(a3+b3)+a(a2+b3)+b(a+b)+2c =(a+b)[(a+b)2-3a b]+a[(a+b)2-2 a b ]+b(a+b)+2c =- =- = (2)证明:由(1)已知,A、B的中点M为( ∴ M(- 又f( =(- =- = = ∴ A、B连线的中点M在y=f(x)上。
|

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
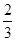 与x=1时都取得极值.
与x=1时都取得极值. 与x=1时都取得极值。
与x=1时都取得极值。