题目内容
在区间[-1,1]上任取两数a、b,求二次方程x2+ax+b=0的两根:(1)都是实数的概率;
(2)都是正数的概率.
分析:因为区间[-1,1]内的数有无限多个,所以本题属于几何概型.但由于作图后发现阴影部分面积不好计算,故可考虑采用均匀随机数模拟试验法计算相应事件的概率.
解:由题意知-1≤a≤1,-1≤b≤1,直线x=±1、直线y=±1围成一个边长为2的正方形.
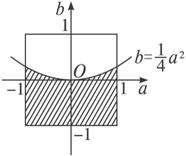
(1)若a、b都是实数,需且只需Δ=a2-4b≥0,即b≤![]() a2,利用随机模拟求概率.
a2,利用随机模拟求概率.
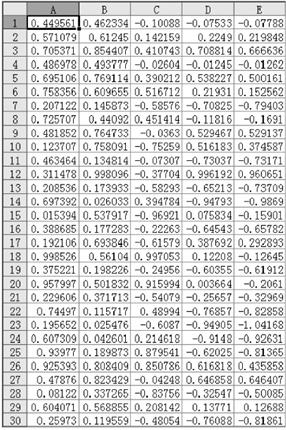
①如右图用Excel软件产生区间[0,1]内的两组随机数a1、b1(共30组);
②经平移和伸缩变换,a=a1*2-1,b=b1*2-1;
③数出满足b≤![]() a2的数组共19组.
a2的数组共19组.
则所求概率约为![]() (N为总数组数).
(N为总数组数).
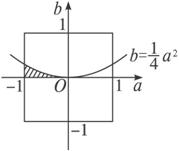
(2)若两根都是正数,则有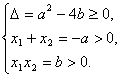
即b≤![]() a2且a<0,b>0.
a2且a<0,b>0.
在第(1)问求出的随机数中数出满足b≤![]() a2且a<0,b>0的数组数共2组,则所求概率约为
a2且a<0,b>0的数组数共2组,则所求概率约为![]() .
.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
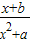 的定义域为R,f(1)=
的定义域为R,f(1)= .
.