题目内容
给定正整数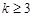 ,若项数为
,若项数为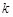 的数列
的数列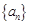 满足:对任意的
满足:对任意的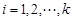 ,均有
,均有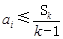 (其中
(其中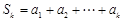 ),则称数列
),则称数列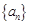 为“Γ数列”.
为“Γ数列”.
(1)判断数列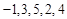 和
和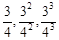 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;
(2)若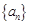 为“Γ数列”,求证:
为“Γ数列”,求证: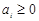 对
对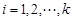 恒成立;
恒成立;
(3)设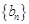 是公差为
是公差为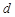 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数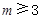 ,
,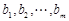
均构成“Γ数列”,求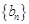 的公差
的公差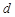 .
.
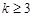 ,若项数为
,若项数为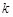 的数列
的数列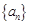 满足:对任意的
满足:对任意的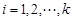 ,均有
,均有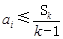 (其中
(其中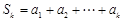 ),则称数列
),则称数列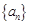 为“Γ数列”.
为“Γ数列”.(1)判断数列
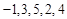 和
和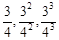 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;(2)若
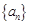 为“Γ数列”,求证:
为“Γ数列”,求证: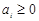 对
对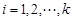 恒成立;
恒成立;(3)设
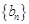 是公差为
是公差为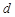 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数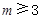 ,
,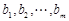
均构成“Γ数列”,求
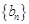 的公差
的公差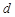 .
.(1)数列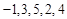 不是“
不是“ 数列”; 数列
数列”; 数列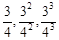 是“
是“ 数列”;(2)详见解析;(3)数列
数列”;(2)详见解析;(3)数列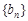 的公差
的公差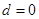 .
.
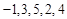 不是“
不是“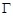 数列”; 数列
数列”; 数列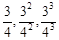 是“
是“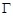 数列”;(2)详见解析;(3)数列
数列”;(2)详见解析;(3)数列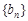 的公差
的公差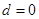 .
.试题分析:(1)判断数列
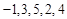 和
和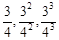 是否是“Γ数列”,根据“Γ数列”的定义,对任意的
是否是“Γ数列”,根据“Γ数列”的定义,对任意的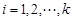 ,均有
,均有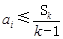 ,只要每一项都满足
,只要每一项都满足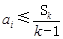 ,就是“Γ数列”,有一项不满足就不是“Γ数列”,对于数列
,就是“Γ数列”,有一项不满足就不是“Γ数列”,对于数列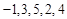 ,
,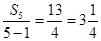 ,观察数列中的项,
,观察数列中的项,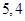 都大于
都大于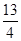 ,顾不符合定义,对于数列
,顾不符合定义,对于数列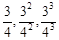 ,
,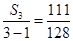 ,观察数列中的每一项,都小于
,观察数列中的每一项,都小于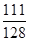 ,符合定义,故是“Γ数列”;(2) 若
,符合定义,故是“Γ数列”;(2) 若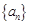 为“Γ数列”,求证:
为“Γ数列”,求证: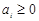 对
对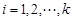 恒成立,本题直接证明似乎无从下手,因此可用反证法,即假设存在某项
恒成立,本题直接证明似乎无从下手,因此可用反证法,即假设存在某项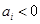 ,把它作为条件,可得
,把它作为条件,可得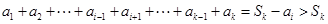 ,设
,设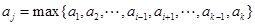 ,得出
,得出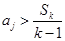 ,显然这与“
,显然这与“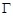 数列”定义矛盾,从而得证;(3)求
数列”定义矛盾,从而得证;(3)求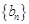 的公差
的公差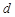 ,由(2)可知
,由(2)可知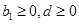 ,分
,分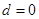 ,与
,与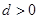 ,两种情况讨论,当
,两种情况讨论,当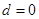 易证符合,当
易证符合,当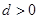 时,显然是递增数列,由“
时,显然是递增数列,由“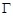 数列”的定义可知
数列”的定义可知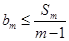 ,即
,即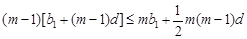 ,整理得
,整理得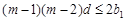 ,当
,当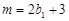 时,不等式不成立,故不是“
时,不等式不成立,故不是“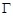 数列”,因此得公差
数列”,因此得公差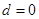 .
.(1)①因为
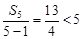 ,数列
,数列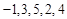 不是“
不是“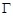 数列”, 2分
数列”, 2分②因为
 ,又
,又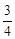 是数列
是数列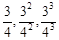 中的最大项
中的最大项所以数列
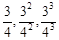 是“
是“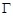 数列”. 4分
数列”. 4分(2)反证法证明:
假设存在某项
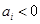 ,则
,则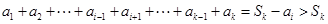 .
.设
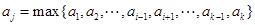 ,则
,则 ,
,所以
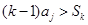 ,即
,即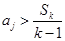 ,
,这与“
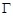 数列”定义矛盾,所以原结论正确. 8分
数列”定义矛盾,所以原结论正确. 8分(3)由(2)问可知
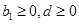 .
. ①当
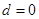 时,
时, ,符合题设; 9分
,符合题设; 9分②当
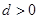 时,
时,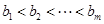
由“
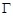 数列”的定义可知
数列”的定义可知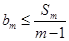 ,即
,即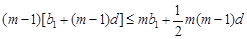
整理得
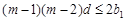 (*)
(*)显然当
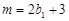 时,上述不等式(*)就不成立
时,上述不等式(*)就不成立所以
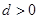 时,对任意正整数
时,对任意正整数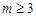 ,
,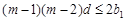 不可能都成立.
不可能都成立.综上讨论可知
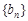 的公差
的公差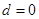 . 13分
. 13分
练习册系列答案
相关题目
 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
. (
( )是常数数列;
)是常数数列; 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 (
(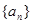 满足:
满足: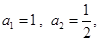 且
且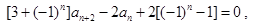
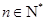 .
.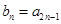 ,判断
,判断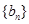 是否为等差数列,并求出
是否为等差数列,并求出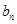 ;
;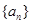 的前
的前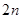 项的和为
项的和为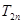 ,求
,求 万元,每年应交保险费,养路费,保险费共
万元,每年应交保险费,养路费,保险费共 万元,汽车的维修费为:第一年
万元,汽车的维修费为:第一年 万元,第二年
万元,第二年 万元,第三年
万元,第三年 万元,……,依次成等差数列逐年递增.
万元,……,依次成等差数列逐年递增. 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为 试写出
试写出 的表达式;
的表达式;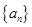 为等差数列,且
为等差数列,且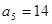 ,
,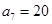 ,数列
,数列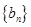 的前
的前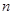 项和为
项和为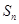 ,
,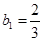 且
且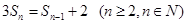
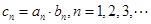 ,求数列
,求数列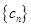 的前
的前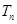 .
. 满足
满足 .
. 项和
项和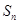 ;
; 成等比数列,求
成等比数列,求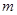 的值.
的值.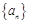 中,
中,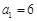 ,且
,且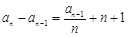 (
(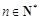 ,
,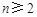 ),则这个数列的
),则这个数列的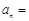 ______________.
______________. 中,
中,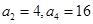 .
.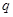 ;
;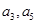 分别为等差数列
分别为等差数列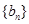 的第3项和第5项,求数列
的第3项和第5项,求数列