题目内容
设数列{an}的通项是关于x的不等式x2-x<(2n-1)x (n∈N*)的解集中整数的个数.数列{an}的前n项和为Sn.
(Ⅰ)求an;
(Ⅱ)设m,k,p∈N*,m+p=2k,求证: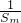 +
+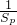 ≥
≥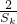 ;
;
(Ⅲ)对于(Ⅱ)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
解:(1)不等式x2-x<(2n-1)x 即x(x-2n)<0,解得:0<x<2n,其中整数有2n-1个,
故 an=2n-1.
(2)由(1)知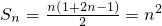 ,∴Sm=m2,Sp=p2,Sk=k2.
,∴Sm=m2,Sp=p2,Sk=k2.
由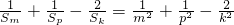 =
= =
=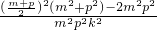
≥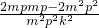 =0,
=0,
即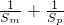 ≥
≥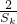 .
.
(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则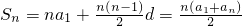 ,
,
∵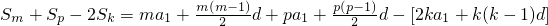 =
=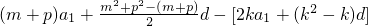 ,
,
把m+p=2k代入上式化简得Sm+Sp-2Sk=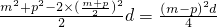 ≥0,…16分.
≥0,…16分.
∴Sm+Sp≥2Sk.
又 Sm•Sp =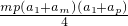 =
=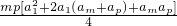
≤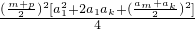 =
=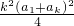 =
=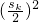 .
.
∴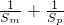 =
=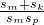 ≥
≥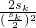 =
=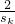 ,故
,故 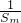 +
+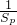 ≥
≥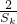 成立.
成立.
分析:(1)由题意知数列{an}的通项是关于x的不等式的解集中整数的个数,题目首先应该解不等式,从不等式的解集中得到整数的个数,得到数列的通项,用等差数列的定义来验证.
(2)根据前面结果写出要用的前几项的和,从不等式的一侧入手,利用均值不等式得到要求的结论.
(3)本题是对上一问的延伸,方法和前面的类似,但题目所给的一般的各项均为正数的等差数列在整理时增加了难度,题目绝大部分工作是算式的整理,注意不能出错.
点评:本题没有具体的数字运算但运算量非常大,它考查的是等差数列和等比数列的性质,基本不等式,实际上这类问题比具体的数字运算要困难,是几个知识点结合起来的综合问题,属于中档题.
故 an=2n-1.
(2)由(1)知
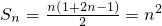 ,∴Sm=m2,Sp=p2,Sk=k2.
,∴Sm=m2,Sp=p2,Sk=k2.由
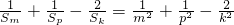 =
= =
=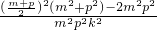
≥
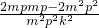 =0,
=0,即
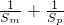 ≥
≥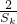 .
. (3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则
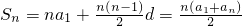 ,
,∵
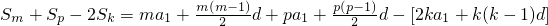 =
=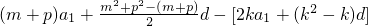 ,
,把m+p=2k代入上式化简得Sm+Sp-2Sk=
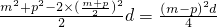 ≥0,…16分.
≥0,…16分.∴Sm+Sp≥2Sk.
又 Sm•Sp =
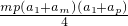 =
=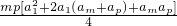
≤
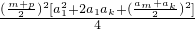 =
=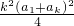 =
=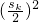 .
.∴
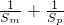 =
=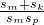 ≥
≥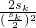 =
=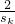 ,故
,故 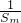 +
+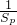 ≥
≥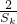 成立.
成立.分析:(1)由题意知数列{an}的通项是关于x的不等式的解集中整数的个数,题目首先应该解不等式,从不等式的解集中得到整数的个数,得到数列的通项,用等差数列的定义来验证.
(2)根据前面结果写出要用的前几项的和,从不等式的一侧入手,利用均值不等式得到要求的结论.
(3)本题是对上一问的延伸,方法和前面的类似,但题目所给的一般的各项均为正数的等差数列在整理时增加了难度,题目绝大部分工作是算式的整理,注意不能出错.
点评:本题没有具体的数字运算但运算量非常大,它考查的是等差数列和等比数列的性质,基本不等式,实际上这类问题比具体的数字运算要困难,是几个知识点结合起来的综合问题,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目