题目内容
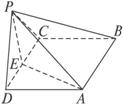
四棱锥P—ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是面积为(1)求证:PA⊥CD;
(2)求二面角PABD的度数.
(1)证明:如图,由题意知AD·DC·sin∠ADC=![]() ,
,
即22·sin∠ADC=![]() .
.
∴sin∠ADC=![]() ,∠ADC=60°.
,∠ADC=60°.
作AE⊥DC于E,连结PE,则DE=1.∴E为DC的中点.
∵PD=PC,∴PE⊥DC.
∵平面PDC⊥底面ABCD,∴PE⊥底面ABCD.
∵DC⊥AE,∴DC⊥PA.
(2)解:∵DC∥AB,AB⊥AE,∴∠PAE为二面角PABD的平面角.
在Rt△ADE中,AD=2,DE=1,
∴AE=![]() .在正三角形PDC中,DC=2,
.在正三角形PDC中,DC=2,
∴PE=![]() .∴tan∠PAE=
.∴tan∠PAE=![]() =1.
=1.
∴∠PAE=45°,即二面角P-AB-D为45°.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
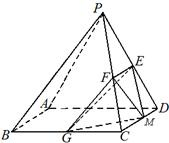 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.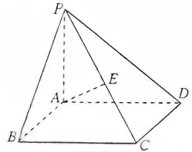 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2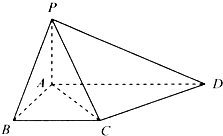 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.