题目内容
10．若（2x+3）4=a0+a1x+a2x2+a3x3+a4x4，则（a0+a2+a4）2-${（{a_1}+{a_3}）^2}$=625．分析 分别令x赋值为1和-1，得到（a0+a2+a4-a1-a3）（a0+a2+a4+a1+a3）．
解答 解：令x=1得到a0+a1+a2+a3+a4=（2+3）4=54，
令x=-1，得到a0-a1+a2-a3-a4=（-2+3）4=1，
则（a0+a2+a4）2-${（{a_1}+{a_3}）^2}$=（a0+a1+a2+a3+a4）（a0-a1+a2-a3+a4）=54=625．
故答案为：625．
点评 本题考查了二项展开式的二项式系数的问题；如此问题经常采用赋值法解答．
练习册系列答案
一本好题口算题卡系列答案
相关题目
20．${∫}_{0}^{\sqrt{2}}$$\sqrt{2-{x}^{2}}$dx=（ ）
| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
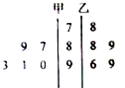如图是甲、乙两位射击运动员的5次训练成绩（单位：环）的茎叶图，则成绩较为稳定（方差较小）的运动员是甲．