题目内容
设p：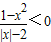
，q：x2+x-6＞0，则p是q的（ ）A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【答案】分析：先将分式不等式转化为整式不等式组，解二次不等式及绝对值不等式组成的不等式组，化简命题p；解二次不等式化简命题q；判断出p，q对应的集合的包含关系，判断出p是q的什么条件．
解答：解：∵
∴
解得-1＜x＜1或x＞2或x＜-2
即命题p：-1＜x＜1或x＞2或x＜-2
∵x2+x-6＞0，
∴x＞2或x＜-3．
即命题q：x＞2或x＜-3．
∵{x|x＞2或x＜-3}?{x|-1＜x＜1或x＞2或x＜-2}，
所以p是q的必要不充分条件．
故选B
点评：解分式不等式关键是将其转化为整式不等式、考查判断一个命题是另一个命题的什么条件，应该先化简两个命题．
解答：解：∵
∴
解得-1＜x＜1或x＞2或x＜-2
即命题p：-1＜x＜1或x＞2或x＜-2
∵x2+x-6＞0，
∴x＞2或x＜-3．
即命题q：x＞2或x＜-3．
∵{x|x＞2或x＜-3}?{x|-1＜x＜1或x＞2或x＜-2}，
所以p是q的必要不充分条件．
故选B
点评：解分式不等式关键是将其转化为整式不等式、考查判断一个命题是另一个命题的什么条件，应该先化简两个命题．
练习册系列答案
相关题目
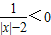，q：x2+x-6＜0，则p是q的（ ）
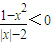，q：x2+x-6＞0，则p是q的（ ）
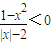，q：x2+x-6＞0，则p是q的（ ）
x∈R，x2＞0总成立，则命题
p：
x∈R，x2≤0总成立；
，q：x2+x-2＞0，则p是q的充分不必要条件；
和
，则
与
的夹角为30°。