题目内容
（本题满分8分） 已知函数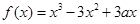
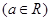在
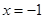处，取得极值
(1) 求实数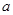
的值 (2) 求函数
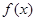的单调区间，并指出其单调性。
【答案】
（1）
（2）函数
在区间
和
上单调递增，在区间
上单调递减
【解析】解：（1）
,由函数 在
处取得极值，得
，解得
3分
(2)由（1）得，令
，得
或
令
，得
，5分
所以函数在区间和上单调递增
在区间上单调递减8分
练习册系列答案
相关题目
，函数
.
的极值(用含
的式子表示)；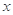
轴有3个不同交点，求
。
的振幅和最小正周期；
时,函数
时，求
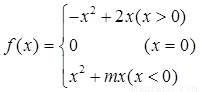
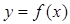的图象；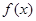
在区间[－1，
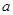－2]上单调递增，试确定
．
的定义域；