题目内容

已知点F₁、F₂分别是椭圆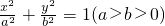 $数学公式$ 的左、右焦点，A、B是以O（O为坐标原点）为圆心、|OF₁|为半径的圆与该椭圆左半部分的两个交点，且△F₂AB是正三角形，则此椭圆的离心率为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

A
分析：根据A、B是以O（O为坐标原点）为圆心、|OF₁|为半径的圆与该椭圆左半部分的两个交点，且△F₂AB是正三角形，确定|F₁A|=c， $\text{[math]}$ ，再利用椭圆的定义可得结论．
解答：由题意，∵A、B是以O（O为坐标原点）为圆心、|OF₁|为半径的圆与该椭圆左半部分的两个交点，
∴|OA|=|OB|=|OF₂|=c
∵△F₂AB是正三角形，
∴ $\text{[math]}$
∴|F₁A|=c，
∵|F₁A|+|F₂A|=2a
∴ $\text{[math]}$
∴ $\text{[math]}$ = $\text{[math]}$
故选A．
点评：本题考查椭圆的性质和应用，考查椭圆的定义，属于基础题．

练习册系列答案

名校调研系列卷期末小综合系列答案

黄冈状元成才路应用题系列答案

小学毕业升学全真模拟卷内蒙古人民出版社系列答案

全优假期作业本快乐暑假系列答案

世纪夺冠导航总复习系列答案

海淀黄冈暑假作业合肥工业大学出版社系列答案

快乐暑假快乐学中原农民出版社系列答案

全程解读系列答案

天下无题系列丛书绿色假期暑假作业系列答案

小学生暑假衔接陕西师范大学出版总社系列答案

相关题目

（2011•聊城一模）已知点F₁，F₂分别为椭圆C：

=1(a＞b＞0)的左右焦点，P是椭圆C上的一点，且|F1F2|=2，∠F1PF2=

，△F1PF2的面积为

（Ⅰ）求椭圆C的方程；
（Ⅱ）点M的坐标为(

，0)，过点F₂且斜率为k的直线l与椭圆C相交于A，B两点，对于任意的k∈R，

是否为定值？若是求出这个定值；若不是说明理由．

（2012•青州市模拟）已知点F₁，F₂分别为椭圆C：

=1(a＞b＞0)的左、右焦点，点P为椭圆上任意一点，P到焦点F₂的距离的最大值为

+1，且△PF₁F₂的最大面积为1．
（ I）求椭圆C的方程．
（ II）点M的坐标为(

，0)，过点F₂且斜率为k的直线L与椭圆C相交于A，B两点．对于任意的k∈R，

是否为定值？若是求出这个定值；若不是说明理由．

已知点F₁，F₂分别为椭圆C：

=1(a＞b＞0)的左、右焦点，点P为椭圆上任意一点，P到焦点F₂（1，0）的距离的最大值为

+1．
（1）求椭圆C的方程．
（2）点M的坐标为（

，0），过点F₂且斜率为k的直线l与椭圆C相交于A，B两点．对于任意的k∈R，

是否为定值？若是求出这个定值；若不是说明理由．

已知点F₁，F₂分别为椭圆C：

（a>b>0）的左、右焦点，点P为椭圆上任意一点，P到焦点F₂的距离的最大值为

+1，且△PF₁F₂的最大面积为1。
（1）求椭圆C的方程。
（2）点M的坐标为

，过点F₂且斜率为k的直线L与椭圆C相交于A，B两点。对于任意的k∈R，

是否为定值？若是求出这个定值；若不是说明理由。

已知点F₁，F₂分别为椭圆C：

的左右焦点，P是椭圆C上的一点，且

（Ⅰ）求椭圆C的方程；
（Ⅱ）点M的坐标为

，过点F₂且斜率为k的直线l与椭圆C相交于A，B两点，对于任意的

是否为定值？若是求出这个定值；若不是说明理由．